1. Binärzahlen und deren Umwandlung
Das Binärsystem bildet die Grundlage für die Welt der Informatik. Deshalb ist es wichtig das Binärsystem zu verstehen, da es die Sprache ist, in der Computer kommunizieren. Dieses System, basierend auf nur zwei Zahlen 0 und 1, mag auf den ersten Blick simpel erscheinen, entfaltet jedoch eine erstaunliche Komplexität und Leistungsfähigkeit, wenn es um die Verarbeitung von Informationen geht. Nachfolgend wird genauer betrachtet, wie das Binärsystem die Grundlage für die digitale Logik bildet und somit die Basis für die Funktionsweise von Computern legt. Dazu gehört der Aufbau der Binärzahlen, das Rechnen mit diesen und die Umwandlung in unser Dezimalsystem.
Aufgabe:
Die Landeswährung von Fantasia sind Fa. Es gibt nur Geldmünzen im Wert von 128 Fa, 64 Fa, 32 Fa, 16 Fa, 8 Fa, 4 Fa, 2 Fa und 1 Fa. Da die Münzen so schön glänzen, versuchen die Einwohner von Fantasia immer den exakten Betrag zu bezahlen aber dabei so wenige Münzen wie möglich zu verwenden. Mit dem nachfolgenden Tool kann man nachstellen, wie sich Geldbeträge in Fa zusammenstellen lassen.
- Ada schaut in ihre Geldbörse. Sie hat jede Münze von 16 Fa bis 1 Fa noch genau einmal. Da die Münzen ganz schön schwer sind überlegt sie, ob sie diese bei der Bank gegen eine 32 Fa-Münze eintauschen kann. Ist dies möglich?
- Ada ist durstig und möchte sich eine Fandaa kaufen. Diese kostet 13 Fa. Welche Geldmünzen sollte sie optimalerweise verwenden, um diesen Betrag zu zahlen?
- Nun hat sie Lust auf ein Eis. Dieses kostet 10 Fa. Kann sie dieses Eis mit ihren verbleibenden Münzen passend bezahlen?
- Das Land Fantasia entscheidet demokratisch, eine neue Geldmünze mit noch höherem Wert einzuführen. Begründe, welche Münze du Fantasia anhand des Währungssystems empfehlen würdest.
Lösung (nur für Lehrer sichtbar)
- Kann Ada ihre Münzen bei der Bank gegen 32 Fa eintauschen? Nein, denn 16+8+4+2+1=31. Ada erreicht die 32 nicht.
- Jeder Münzwert kann höchstens einmal verwendet werden. In Summe muss genau 13 herauskommen. Sie muss die Münzen 8+4+1=13 verwenden.
- Kann sie mit ihren verbliebenen Münzen ein Eis für 10 Fa passend bezahlen? Sie hat noch eine 16Fa- und eine 2Fa- Münze übrig. Zusammen ergibt das 18Fa. Das ist zwar genug für das Eis, jedoch kann sie nicht passend zahlen.
- Wenn man jede Geldmünze nur einmal verwenden dar, kann man mit den bisherigen Münzen höchstens den Betrag 128+64+32+16+8+4+2+1=255 erreichen. Also sollte als nächstes eine Münze mit dem Wert 256Fa eingeführt werden. Der Wert der nächsten Geldmünze ist also immer doppelt so hoch wie der Wert der vorherigen Münze.
Alle Münzwerte im obigen Beispiel sind das Ergebnis einer Zweierpotenz. Angefangen bei 1 wird der Wert immer wieder verdoppelt, um auf die nächste Zahl zu kommen. Man summiert nur diejenigen Münzen, die tatsächlich verwendet werden. Dies ist das Prinzip, welches dem Binärsystem zugrunde liegt. Eine Binärzahl besteht dabei aus den Ziffern 0 und 1, zum Beispiel 10010. Auf das Münzbeispiel übertragen, würde dies bedeuten, dass man bei 1 die Münze verwendet und bei 0 nicht, also eine 16 Fa-Münze und eine 2 Fa-Münze. Im Falle des Computers steht die 1 für "Strom an" und 0 für "Strom aus". Die Werte der Ziffern entsprechen absteigend sortierten Zweierpotenzen, die immer bei 20, also 1 enden. 16=24 und 2=21.
1.1 Umwandlung von Zahlen
Binärsystem Im Binärsystem bestehen alle Zahlen nur aus den Ziffern 0 und 1. Es ist ein Stellenwertsystem zur Basis 2. Entsprechend bilden sich alle Binärzahlen aus Kombinationen von Zweierpotenzen, also: 20=1, 21=2, 22=4, 23=8, 24=16, 25=32, 26=64, 27=128 usw. .
Beispiel:
11001 = 1x24 + 1x23 + 0x22 + 0x21 + 1x20 = 1x16 + 1x8+ 0x4 + 0x2+ 1x1 = 25
120 = 1x64 + 1x32 + 1x16 + 1x8 + 0x4 + 0x2 + 0x1 = 1x26 + 1x25 + 1x24 + 1x23 + 0x22 + 0x21 + 0x20 = 1111000
Tipp:
Überlege dir beim Umwandeln ins Binärsystem als erstes, welches die größte Binärzahl ist, die in meine Dezimalzahl hineinpasst. Bei der 120 wäre die 128 zu groß. Die Größtmögliche ist also die 64. Nun gehst du (in der richtigen Reihenfolge) alle Binärzahlen die kleiner sind einmal durch und schreibst je nachdem ob du sie gebrauchen kannst eine 1 oder eine 0 an die entsprechende Stelle.
Eine Tabelle kann bei solchen Übungen durchaus helfen. Der Tabellnkopf sähe dann so aus:
| ... | 23 | 22 | 21 | 20 |
|---|---|---|---|---|
| ... | 8 | 4 | 2 | 1 |
Nun kann darunter für jede Zweierpotenz eingetragen werden, ob ich sie benötige (1) oder nicht (0).
Aufgabe 1: Umwandlung Dezimal-Binär
Wähle die Zweierpotenzen aus, mit deren Hilfe du die Dezimalzahl bilden kannst.
Aufgabe 2: Umwandlung beliebig
Wandle jeweils in das andere Zahlensystem um.
Aufgabe 3: Spiel Umwandlung
Wandle jeweils in das andere Zahlensystem um.
Die Darstellung von Binärzahlen mit den Fingern ist eine einfache und intuitive Methode, um das Binärsystem zu verstehen. Dabei repräsentiert jeder ausgestreckte Finger eine Zweierpotenz, beginnend von rechts mit 20.
Ein ausgestreckter Finger (oder "hoch") bedeutet, die entsprechende Potenz von 2 wird zur Summe addiert. Dies entspricht einer 1 in der Binärdarstellung.
Ein gekrümmter Finger (oder "runter") bedeutet, die entsprechende Potenz von 2 wird nicht addiert. Dies entspricht einer 0 in der Binärdarstellung.
Mit einer Hand kannst du also Binärzahlen von 0 bis 1+2+4+8+16=31 darstellen. Nutzt du beide Hände, kannst du sogar bis 2 10−1=1023 zählen!
1.2 Umwandlung von Zeichen/ Text
Bisher wurde die Darstellung von Zahlen im Binärsystem und deren Umwandlung in das uns vertraute Dezimalsystem behandelt. Computer verarbeiten jedoch nicht nur Zahlen, sondern auch eine Vielzahl anderer Informationen, darunter Texte, Bilder und Töne. Die Frage, die sich nun stellt, ist, wie beispielsweise ein Buchstabe oder ein Satzzeichen in eine Form gebracht werden kann, die ein Computer verstehen und verarbeiten kann, also ebenfalls in eine Folge von Binärziffern. Wie schon beim Thema Digitalisierung beschrieben, wird hierfür meist der ASCII-Code (American Standard Code for Information Interchange) verwendet, der es ermöglicht, Textinformationen in binärer Form darzustellen und somit auch diesen für Computer lesbar zu machen. So steht die 65 beispielsweise für 'A' und die 97 für 'a'.
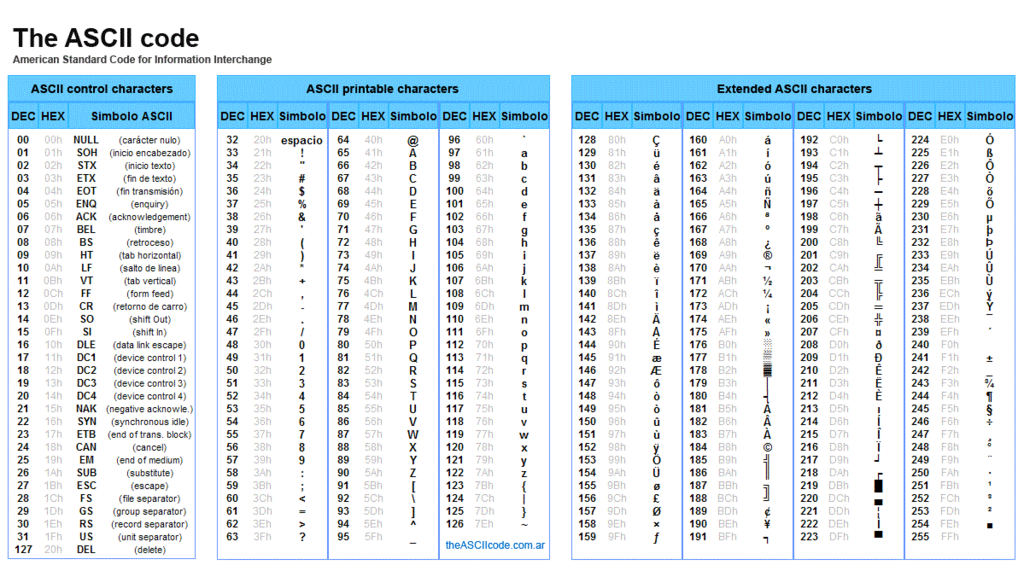
Ein Beispiel:
Hi! = 72 105 33 = 01001000 01101001 00100001
Wichtig ist, dass jedes Zeichen 8 Stellen hat, damit immer klar ist, wo ein Zeichen endet und ein Neues beginnt. Es müssen also ggf. führende Nullen aufgefüllt werden.
Ein anschauliches Beispiel wie das Ganze früher mit Lochkarten realisiert wurde, findet ihr bei den Kollegen von Serlo.
Aufgabe 1: Umwandlung Buchstaben - Binär
Aufgabe 2: geheime Botschaft
Überlege dir einen kurzen Text (5-10 Zeichen) und übersetze ihn wie im Beispiel mit Hilfe der ASCII-Tabelle in den Binärcode. Denke daran, dass jedes Zeichen aus 8 Stellen bestehen muss. Schreibe diesen Code auf einen Zettel und tausche ihn mit einer anderen Person. Übersetzt nun jeweils die Nachricht des anderen wieder in für uns lesbare Buchstaben.
Aufgabe 3: Entschlüssele die geheime Botschaft
