4.2 Gepunktete Kreise
»Kreispunkte im rechtwinkligen Koordinatensystem«
Die Koordinaten eines Kreispunktes in einem rechtwinkligen (kartesischen) Koordinatensystem können mithilfe des Kosinus (cos) und Sinus (sin) ermittelt werden.
- Voraussetzung ist, dass die Definitionen des Kosinus (cos) und des Sinus (sin) eines Winkels im rechtwinkligen Dreieck bekannt sind.
- In der Abbildung 1 ist das rechtwinklige Dreieck mit dem Winkel φ, der Hypotenuse, Ankathete und Gegenkathethete dargestellt.
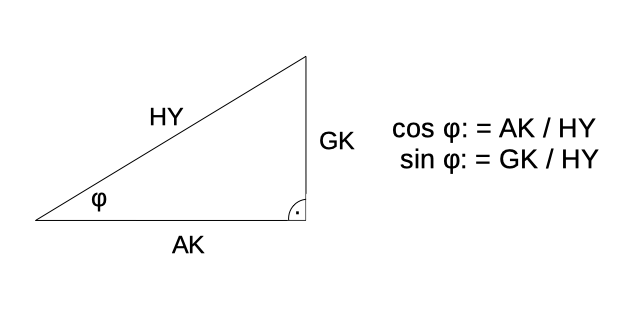
Wie die Koordinaten eines Kreispunktes in einem rechtwinkligen Koordinatensystem mithilfe des Kosinus und Sinus
des Winkel φ ermittelt werden können, ist in der Abbildung 2 gegeben.
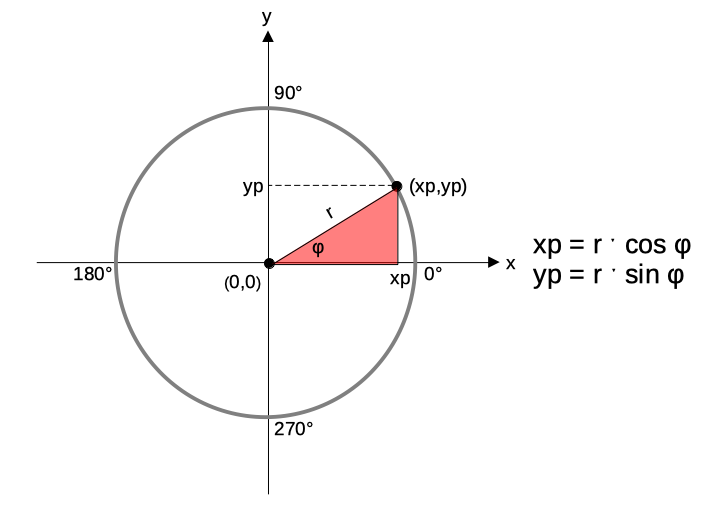
Wie bereits erwähnt, besteht das virtuelle Koordinatensystem des Canvas-Widget aus der positiven
- In der Abbildung 3 ist der Kreis im virtuellen Koordinatensystem des Canvas-Widget mit der nach unten gerichteten positiven y-Achse dargestellt.
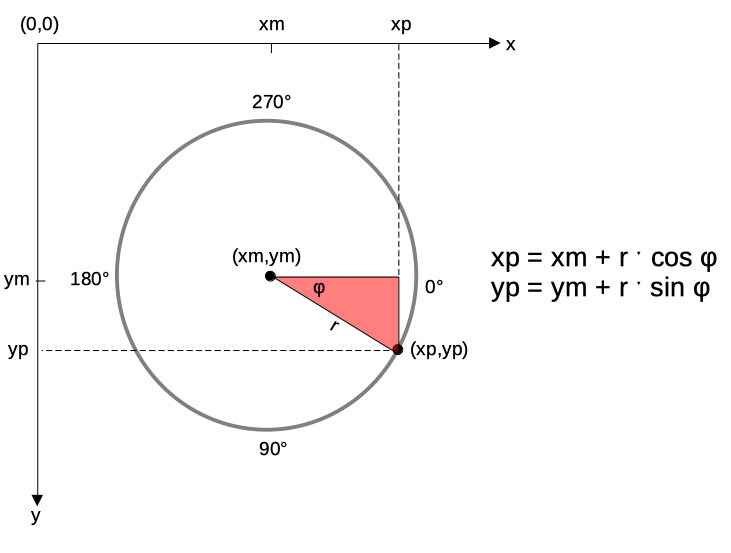
Zum Zeichnen der einzelnen Punkte eines Kreises auf dem Canvas-Widget (Abbildung 1) können deren Koordinaten im Koordinatensystem des Canvas-Widget verwendet werden.

Programm »kreisgrafik1.py«
import tkinter as tk
import math
# Funktion
def zeichnen():
xm=200
ym=200
radius=150
for winkel in range(0, 360, 10):
xp=int(xm+radius*math.cos(math.radians(winkel)))
yp=int(ym+radius*math.sin(math.radians(winkel)))
canvas.create_oval((xp-3, yp+3), (xp+3, yp-3),\
fill="yellow")
# grafische Benutzeroberfläche
root=tk.Tk()
root.title("Kreispunkt Grafik")
root.geometry("400x400")
root.resizable(False, False)
canvas=tk.Canvas(root, background="blue")
# Funktionsaufruf
zeichnen()
canvas.pack(fill=tk.BOTH, expand=True)
root.mainloop()
| 2. Zeile | Das Modul »math« wird in das Programm eingebunden, um die Methoden »sin«, »cos« und »radians« zu nutzen. |
| 4. bis 13. Zeile | Die Funktion »zeichnen« wird deklariert. |
| 6., 7. und 8. Zeile | Der Mittelpnunt des Kreises ist (xm,ym) und der Radius beträgt 150 Pixel. |
| 9. bis 13. Zeile |
Die for-Schleife zum Berechnen der Koordinaten und Zeichnen von 36 Kreispunkten.
|
| 9. Zeile | Der Bereich der Funktion »range« umfasst die Winkel 0°, 10°, 20° … 340°, 350°. |
| 10. und 11. Zeile |
Die Koordinaten xp und yp des Kreispunkts werden mit den Methoden »sin« sowie
»cos« berechnet.
|
| 12. und 13. Zeile | Mit Hilfe der Methode »create_oval« werden die Punkte als kleine Kreise mit Radien von 3 Pixel gezeichnet. |
| 24. Zeile | Die Funktion »zeichnen« wird aufgerufen. |
Aufgabe A53
Implementiere das Programm »kreisgrafik1.py« am Computer, das die in der Abbildung 2 dargestellte Grafik zeichnet.
Führe das Programm aus und teste, ob es fehlerfrei läuft und den gestellten Anforderungen entspricht.
Erweitere das Programm, sodass die in der Abbildung 2 dargestellte Kreispunkte Grafik gezeichnet wird.

Führe das erweiterte Programm aus und teste, ob es fehlerfrei läuft und den gestellten Anforderungen entspricht.
Das folgende Problem wurde bereits mehrmals erwähnt, denn auf dem Canvas-Widget ist die y-Ache des virtuellen
Koordinatensystems nach
- Das heißt, ein Kreis aus Punkten steht aufgrund der nach unten gerichteten y-Achs am Bildschirm für den Betrachter auf dem Kopf.
- Allerdings wird das beim Betrachten der Punkte eines 360° Vollkreises am Bildschirm nicht als störend empfunden.
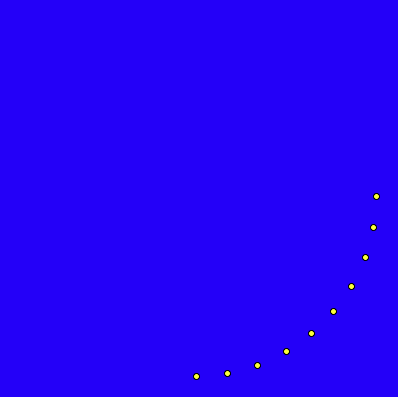
- Anders ist es dagegen beim Betrachten des Vierrtelkreises in der Abbildung 4, dessen Punkte beispielsweise von 0° bis 90° jeweils um 10° nach unten versetzt sind.
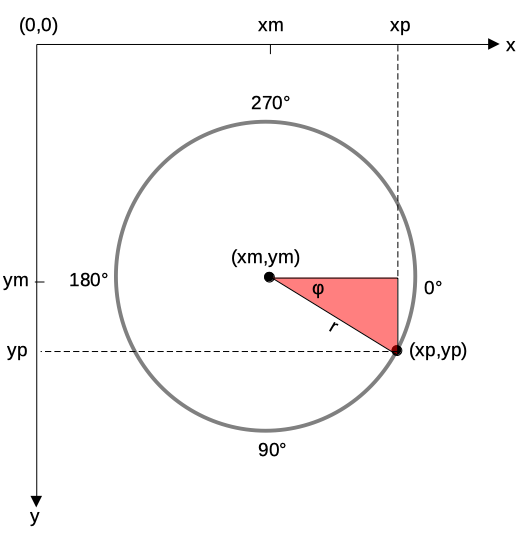
Programm »kreisgrafik2.py«
In der Abbildung 5 ist dargestellt, wie die Koordinaten der Kreispunkte mit den Koordinaten des Kreismittelpunkts durch Linien miteinander verbunden sind.
- Die Kreispunkte für sich sind dabei nicht nicht gezeichnet, sondern einzig die Linien.

Aufgabe A54
Implementiere das Programm »kreisgrafik2.py« am Computer, das die in der Abbildung 5 dargestellte Grafik zeichnet.
Führe das Programm aus und teste, ob es fehlerfrei läuft und den gestellten Anforderungen entspricht.
Erweitere das Programm, sodass die in der Abbildung 6 dargestellte Grafik gezeichnet wird.

Führe das erweiterte Programm aus und teste, ob es fehlerfrei läuft und den gestellten Anforderungen entspricht.
Programm »kreisgrafik3.py«
Aufgabe A55
Implementiere ein Programm »kreisgrafik3.py« am Computer, das die in der Abbildung 7 dargestellte Grafik – mit zufälligen Farben – zeichnet.

Führe das Programm aus und teste, ob es fehlerfrei läuft und den gestellten Anforderungen entspricht.
Programm »kreisgrafik4.py«
Aufgabe A56
Die in der Abbildung 8 dargestellte Grafik besteht aus:
- den roten Punkten des inneren Kreises
- die roten Punkte sind die Mittelpunkte der äußeren Kreise
- die äußeren Kreise bestehen aus gelben Punkten
Damit sich die sechs äußeren Kreise berühren folgende Fragen:
- Welchen Radius muss jeder äußere Kreis haben?
- Welchen Radius muss der innere Kreise haben?
- Wie groß muss der Winkel zwischen jeweils zwei Punkten des inneren Kreises sein?

Implementiere ein Programm »kreisgrafik4.py« am Computer, das die in der Abbildung 8 dargestellte Grafik zeichnet.
Führe das Programm aus und teste, ob es fehlerfrei läuft und den gestellten Anforderungen entspricht.
Programm »kreisgrafik5.py«
Aufgabe A57
Implementiere das Programm »kreisgrafik5.py« am Computer, das die in der Abbildung 9 dargestellte Grafik – mit zufälligen Farben – zeichnet.
- Versuche dabei, dass keine Linie mehrfach gezeichnet wird.

Führe das Programm aus und teste, ob es fehlerfrei läuft und den gestellten Anforderungen entspricht.
