2. Rechnen im Binärsystem
Es ist nun bekannt, wie das Binärsystem funktioniert und warum es für Computer so wichtig ist. Dezimalzahlen können in Binärzahlen umwandelt werden und umgekehrt. Damit sind die Grundlagen gelegt, wie Daten im Inneren eines Computers dargestellt und gespeichert werden.
Doch sollen Daten im Computer nicht nur gespeichert, sondern auch verarbeitet werden. Dies geschieht unter anderem durch das Durchführen von arithmetischen und logischen Operationen. Zu den arithmetischen Operationen zählen Addition, Subtraktion, Multiplikation und Division. Dabei ist schnell festzustellen, dass diese Berechnungen im Binärsystem sehr ähnlich sind zum schriftlichen Rechnen im Dezimalsystem. Es müssen nur wenige Regeln beachtet werden. Wichtig ist außerdem stellenwertgerecht zu rechnen.
2.1 Addition
Bei der Addition werden beide Zahlen stellenwertgerecht untereinandergeschrieben. Für die Berechnung wird bei der kleinsten Stelle begonnen und unter Beachtung der 4 Regeln Schritt für Schritt addiert.
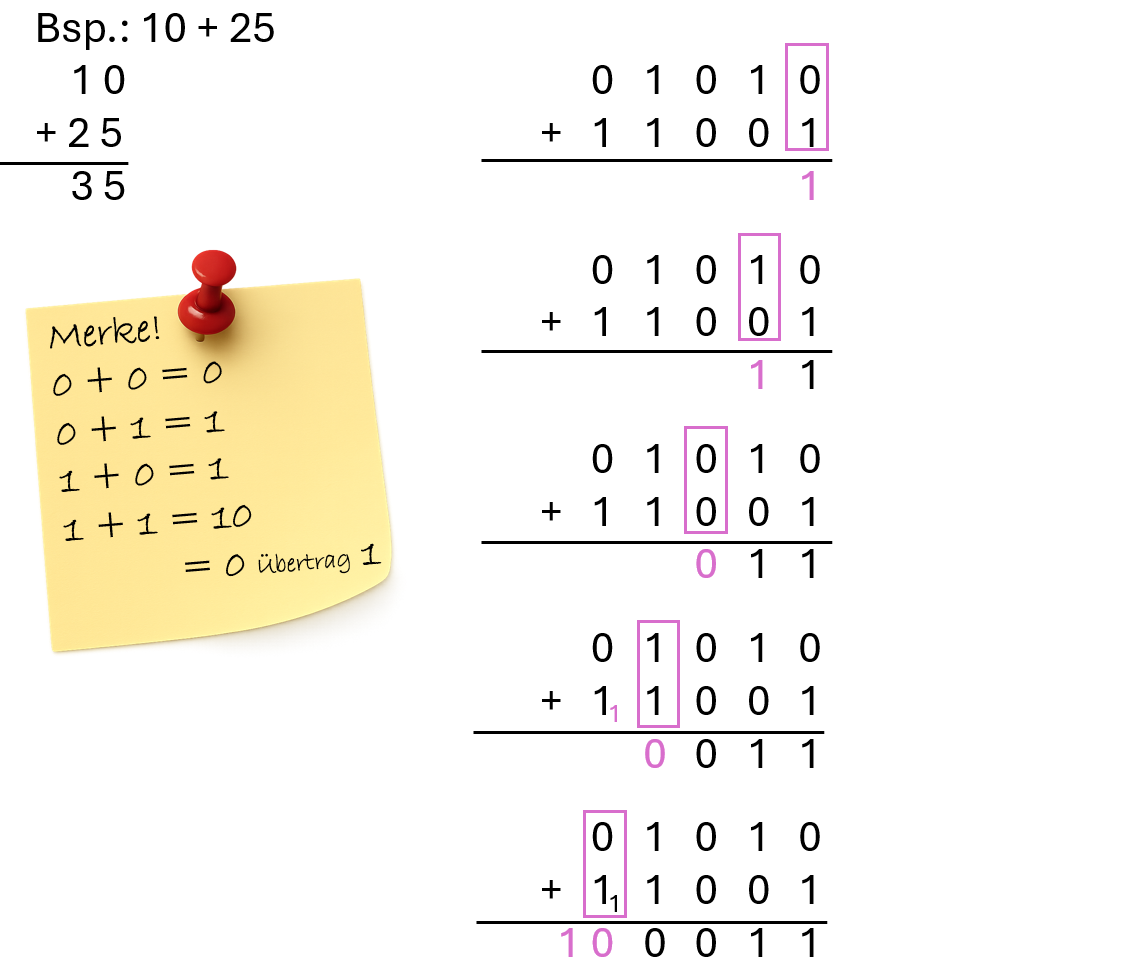
Aufgabe 1:
Addiere schriftlich. Trage deine Ergebnisse zum Überprüfen ein.
Bei binären Berechnungen ist zu beachten, dass sie nur innerhalb des deklarierten Wertebereichs korrekt funktionieren. Im Gegensatz zur realen Welt, in der theoretisch beliebig große Zahlen dargestellt werden können, ist dies in der Informatik aufgrund des begrenzten Speicherplatzes nicht möglich. Der darstellbare Wertebereich ist daher durch den verwendeten Datentyp eingeschränkt. Bei einer Bitbreite von 8 Bit entspricht die größte darstellbare Zahl dem Binärwert 11111111, was dem Dezimalwert 255 entspricht. Wird zu diesem Wert der Binärwert 00000001 (also 1) addiert, ergibt sich 00000000 – also 0. Dies lässt sich durch die Rechenregel erklären, dass 1 + 1 im Binärsystem den Wert 10 ergibt – also 0 mit einem Übertrag von 1. In diesem Fall entsteht beim Rechenergebnis zwar ein Übertrag, dieser kann jedoch aufgrund des festen Speicherrahmens nicht gespeichert werden, wird daher verworfen und das Ergebnis ist „nur“ 0. Sobald der maximal darstellbare Wert erreicht ist, beginnt der Zählvorgang beim kleinsten darstellbaren Wert erneut. Bei fortlaufender Addition von Eins durchläuft das System also immer wieder den Wertebereich von 0 bis 255, beginnend bei 0, endend bei 255, und wieder zurück zu 0 – und immer so weiter.
2.2 Subtraktion
Um Binärzahlen zu subtrahieren kann man zwei verschiedene Varianten nutzen. Eine ist die Komplement-Methode, bei der man das Zweierkomplement des Subtrahenden bildet und anschließend diesen mit der ersten Zahl addiert.
Im Folgenden wird die „Borgen“-Methode erklärt, die etwas intuitiver ist, da die Berechnung größtenteils, wie die von Dezimalzahlen funktioniert. Es muss lediglich eine spezielle Regel beachtet werden. Diese beschreibt, wie im Fall einer Subtraktion der Form „0 - 1“ ein sogenanntes Borgen von der nächsthöheren Stelle erfolgt.
Damit 0 - 1 gerechnet werden kann, muss man sich von der nächsthöherwertigen Stelle (links) eine 1 "borgen".
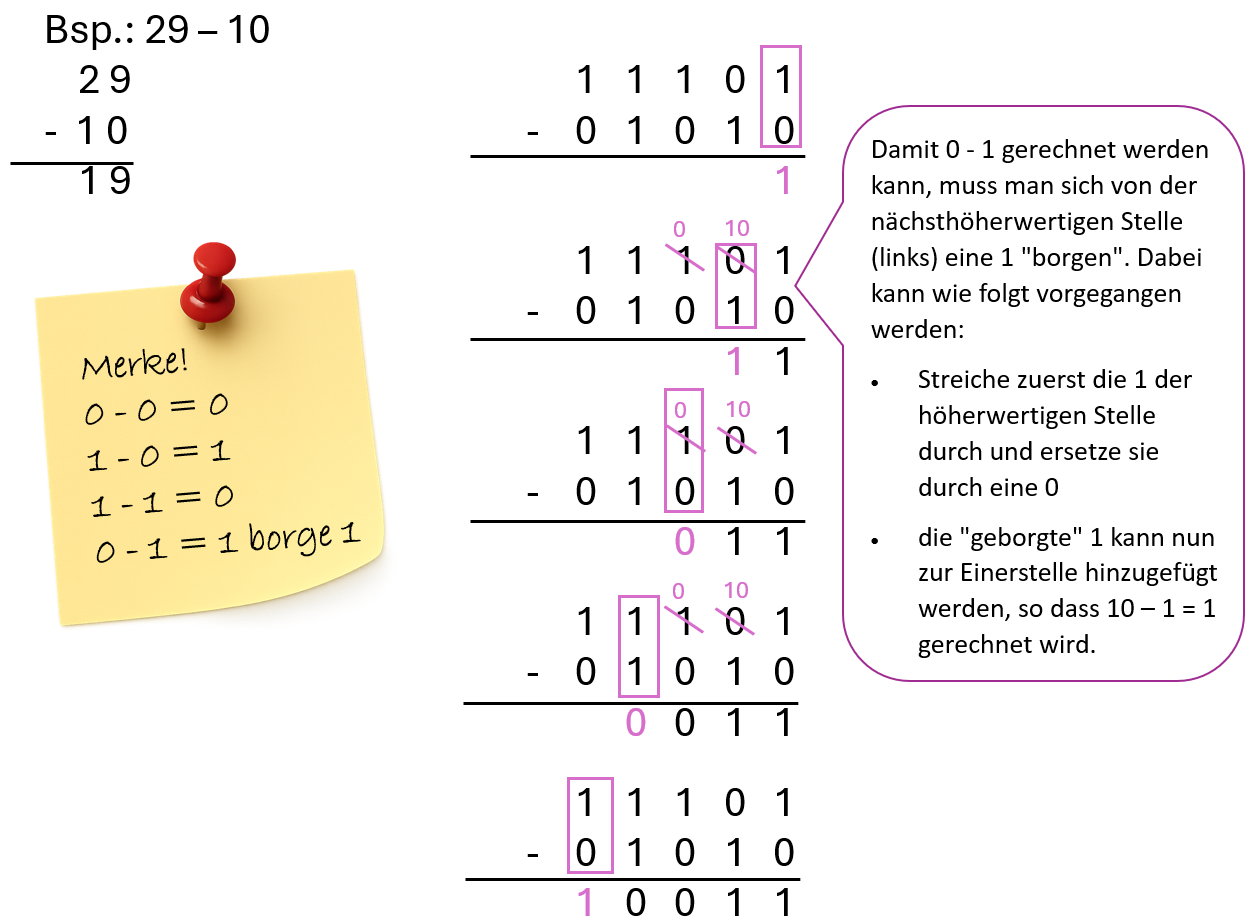
Das Borgen funktioniert falls nötig auch mit mehreren Stellen nacheinander.
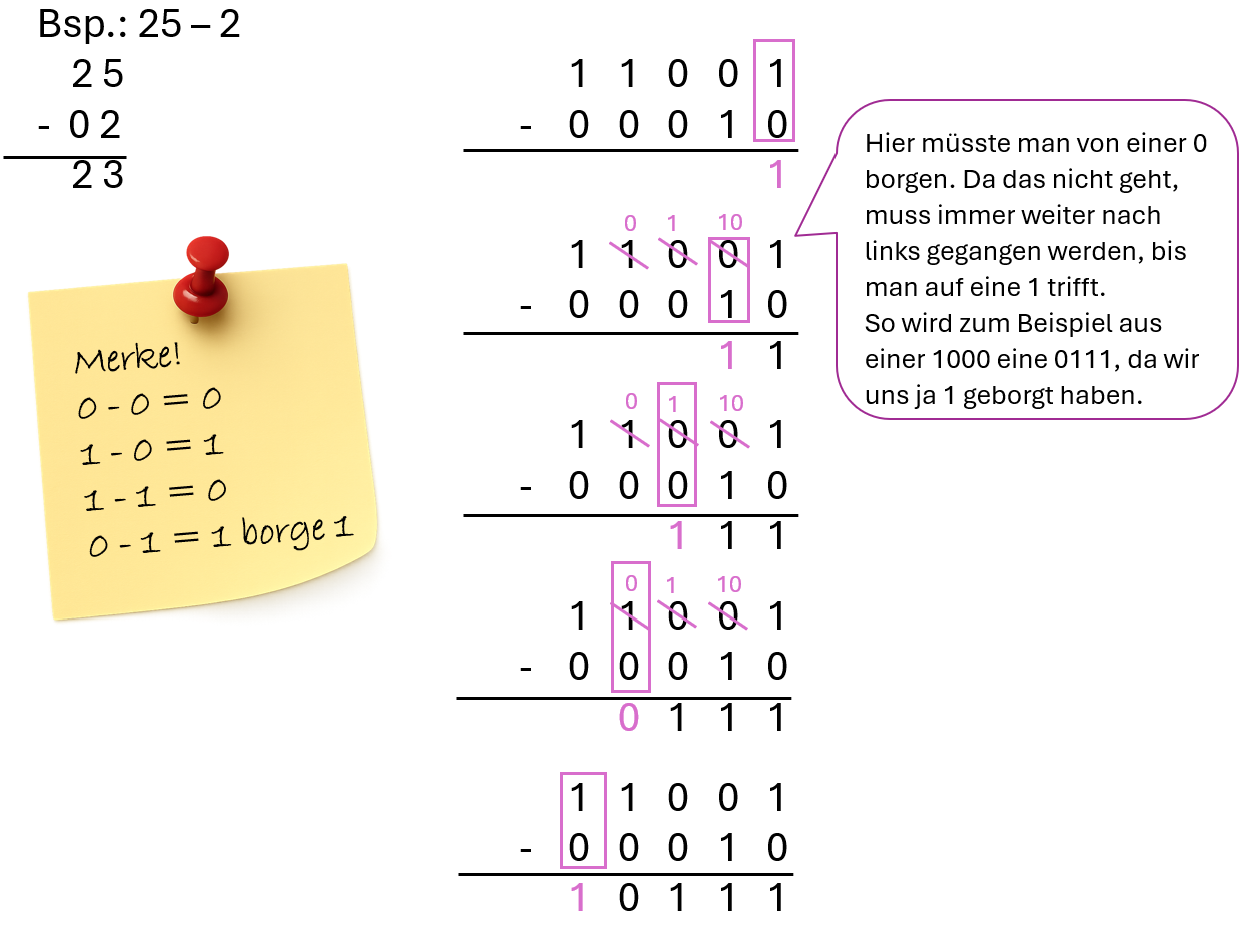
Aufgabe 1:
Subtrahiere schriftlich. Trage deine Ergebnisse zum Überprüfen ein.
2.3 Multiplikation
Auch für die Multiplikation gibt es zwei verschiedene Möglichkeiten. Die intuitivste Variante ist auch hier das schriftliche Multiplizieren, welches genauso funktioniert wie im Dezimalsystem. Der zweite Faktor wird Stelle für Stelle mit dem Ersten multipliziert. Dabei werden die jeweiligen Zwischenergebnisse stellenwertgerecht untereinandergeschrieben. Sind alle Stellen abgearbeitet, werden die Zwischenergebnisse addiert.
Tipp: Falls die kürzere (kleinere) Zahl vorne steht, ist es sinnvoll diese mit der hinteren Zahl zu tauschen, da dann der Rechenweg etwas kürzer wird.
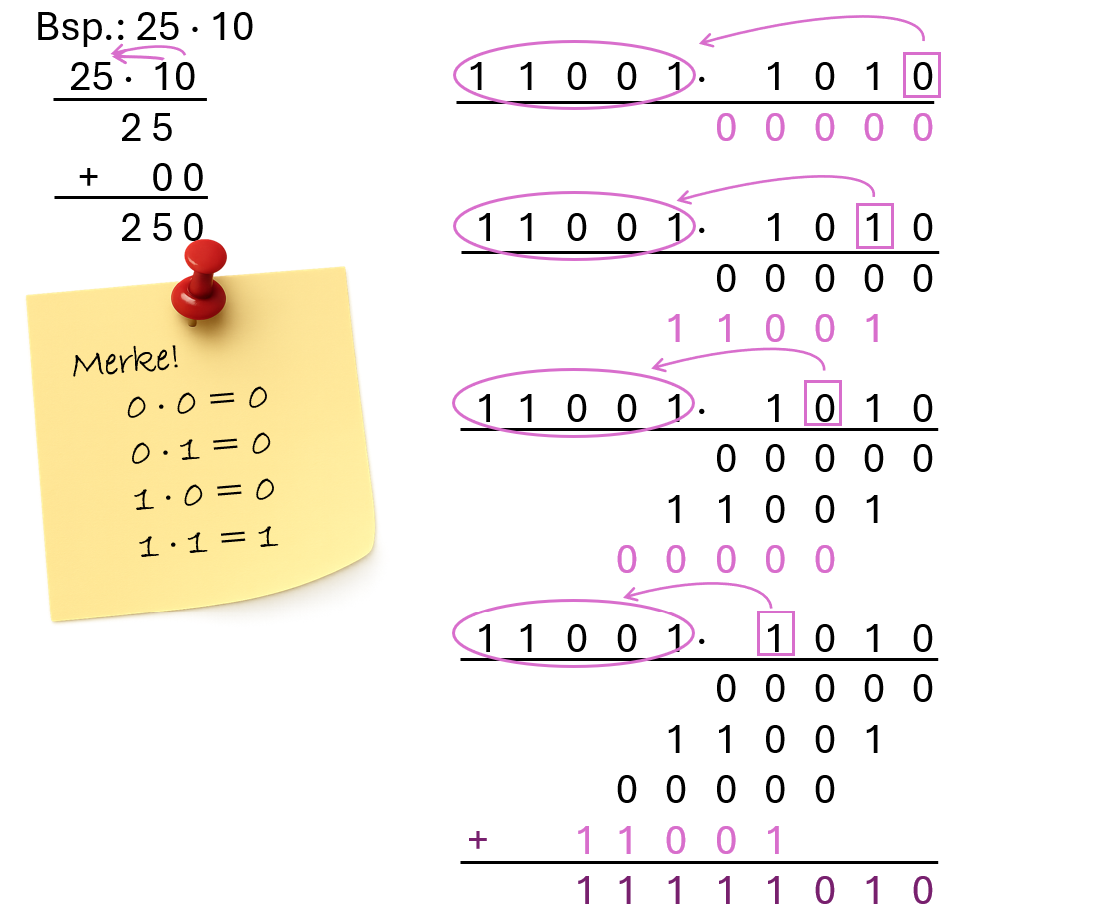
Aufgabe 1:
Multipliziere schriftlich. Trage deine Ergebnisse zum Überprüfen ein.
2.4 Exkurs: Division
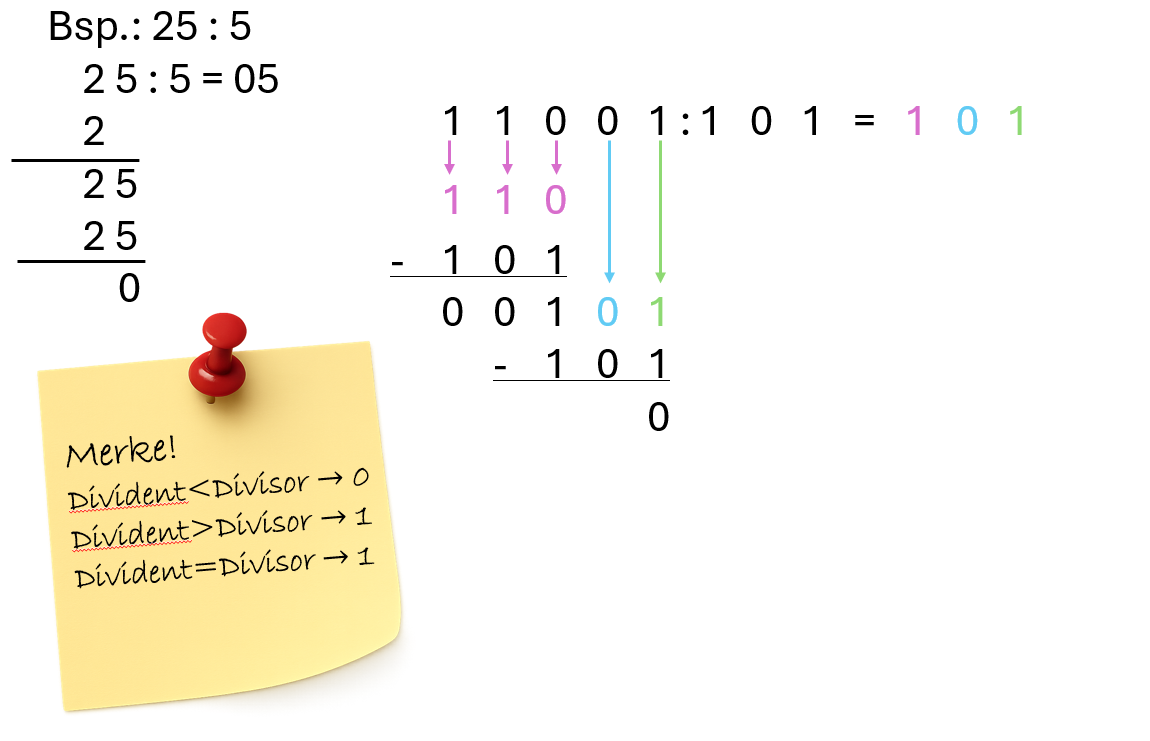
Auch die Division im Binärsystem funktioniert genau wie im Dezimalsystem. Das einfache hier ist: es muss lediglich geschaut werden, ob der Divident in die aktuelle Zahl hineinpasst oder nicht ( 0 oder 1). Begonnen bei der größtwertigen Stelle, wird geschaut, wieviele Stellen man benötigt, damit der Divisor hineinpasst. Diese werden zuerst nach unten gezogen und im Ergebnis wird eine 1 vermerkt. Die Differenz aus dem heruntergezogenen Stellen und dem Divisor wird ermittelt und die nächste Stelle ergänzt. Passt der Divisor in die neue Zahl, wird im Ergebnis eine 1 vermerkt. Passt er nicht, vermerkt man eine 0 und zieht die nächste Stelle nach unten. Dies wird solange durchgeführt, bis der Dividend keine Stelle mehr übrig hat und der Rest 0 ist.
Aufgabe 1:
Dividiere schriftlich. Trage deine Ergebnisse zum Überprüfen ein.
2.5 Queer Beet
Aufgabe 1: Partnerarbeit
Führt jede Grundrechenart einmal aus. Nehmt euch dazu zwei Würfel und würfelt jeweils zwei Zahlen. Wandelt diese ins Binärsystem um und berechnet (jeder für sich) das Ergebnis.
- Addition und Subtraktion: beide Zahlen werden aus jeweils zwei Würfelziffern zusammengesetzt
- Multiplikation und Division: die erste Zahl besteht aus zwei Würfelziffern, die zweite aus einer (natürlich > 1)
- Achtet darauf, dass sich die Zahlen bei der Division auch teile lassen.
