3. negative Binärzahlen

Stellen wir uns vor, wir rechnen im Dezimalsystem 3 - 5. Es ist sofort bekannt, dass das Ergebnis -2 ist. Aber wie funktioniert das, wenn im Binärsystem eine größere Zahl von einer kleineren subtrahiert werden soll?
Der Comic hat gezeigt, dass bei einer Rechnung wie 101−110 etwas Komisches passiert, wenn man sich nur auf die gewohnte Subtraktionsmethode verlässt. Das Ergebnis sieht unerwartet aus und es ist unklar, wie es interpretiert werden soll.
Genau hier beginnt die Reise in die Welt der negativen Binärzahlen. Nachfolgend wird betrachtet, wie Computer dieses Problem lösen und welche cleveren Tricks es gibt, um negative Zahlen darzustellen und mit ihnen zu rechnen. Hierdurch wird klar, warum die scheinbar unmögliche Rechnung 101−110 doch ein klares Ergebnis hat.
3.1 das Vorzeichenbit
Bei vorzeichenbehafteten Binärzahlen kennzeichnet das höchste Bit – auch Most Significant Bit (MSB) genannt – das Vorzeichen der dargestellten Zahl. Ein Vorzeichenbit mit dem Wert 0 steht für eine positive Zahl, ein Wert von 1 für eine negative Zahl.
Beispiel (4 Bit Breite):
0101 entspricht der Dezimalzahl +5 (Vorzeichenbit 0 → positiv)
1101 entspricht der Dezimalzahl -5 (Vorzeichenbit 1 → negativ)
In der sogenannten Vorzeichendarstellung besteht eine Binärzahl aus zwei Bestandteilen:
1. Vorzeichenbit (erstes Bit von links):
0 → positive Zahl
1 → negative Zahl
2. Betragsbits (die restlichen n–1 Bits):
Kodieren den Betrag der Zahl (also den Wert ohne Vorzeichen)
Darstellbarer Zahlenbereich bei n Bit:
Bei 4 Bit liegt der Bereich zwischen -7 (1111) und +7 (0111) Besonderheit: Die Null kann in zwei Formen auftreten: +0 (0000) und -0 (1000)
Beispiel für eine 8-Bit-Darstellung:
+53 = 00110101 (MSB = 0)
-53 = 10110101 (MSB = 1, restliche Bits entsprechen dem Betrag)
Aufgabe 1: Vorzeichenbit-Übung
Wandle die folgende Dezimalzahl in eine 6-Bit Binärzahl mit Vorzeichenbit um.
Aufgabe 2: Vorzeichenbit-Übung
Leider gibt es bei dieser Methode ein paar Haken.
- Das Problem der doppelten Null:
Bei einer festgelegten Bitlänge existieren zwei Darstellungen für die Zahl Null:
- Die positive Null, zum Beispiel 0000 bei 4 Bits.
- Die negative Null, zum Beispiel 1000 bei 4 Bits.
-
Komplexität der Arithmetik:
Die Addition und Subtraktion sind mit dieser Methode aufwendiger, da für negative Zahlen spezielle Regeln und Abläufe erforderlich sind. Eine einfache bitweise Addition, wie sie bei positiven Zahlen funktioniert, führt bei der Einbeziehung negativer Werte zu falschen Ergebnissen.
Beispiel:
(+3) + (-2) = (+1)
0 011 + 1 010 = 1 101 ≠ 1
3.2 das Zweierkomplement
Beim Einerkomplement wird jedes Bit der positiven Zahl invertiert, um das negative Gegenstück zu erhalten. 0001 (Dezimal 1) wird zu 1110 (Dezimal -1 im Einerkomplement). Dabi besteht jedoch immer noch das Problem mit der doppelten Null.
Im Zweierkomplement, das heute als Standard gilt, geschieht nach der Invertierung noch eine Addition von 1. Dadurch ergibt sich ein eindeutiges Muster ohne doppelte Null und ermöglicht eine einfache Binärarithmetik.
Auch beim Zweierkomplement kennzeichnet das Vorzeichenbit mit Wert 1 eine negative Zahl.
Die Umwandlung einer positiven Zahl in ihre negative Entsprechung im Zweierkomplement erfolgt in drei einfachen Schritten:
- positive Dezimalzahl in Binärzahl umwandeln: (Dabei muss die Bitlänge festgelegt sein, z. B. 8 Bit)
- Invertierung (Einerkomplement): jede 0 wird zu einer 1 und jede 1 zu einer 0
- Addition von 1: Zu dem Ergebnis des zweiten Schritts wird der Wert 1 addiert
Beispiel: -5 im Zweierkomplement
- pos. Zahl in binär: +5 = 00000101
- Invertieren: 00000101 → 11111010
- 1 addieren: 11111010 + 1 = 11111011
Aufgabe: Zweierkomplement
Visualisierung:
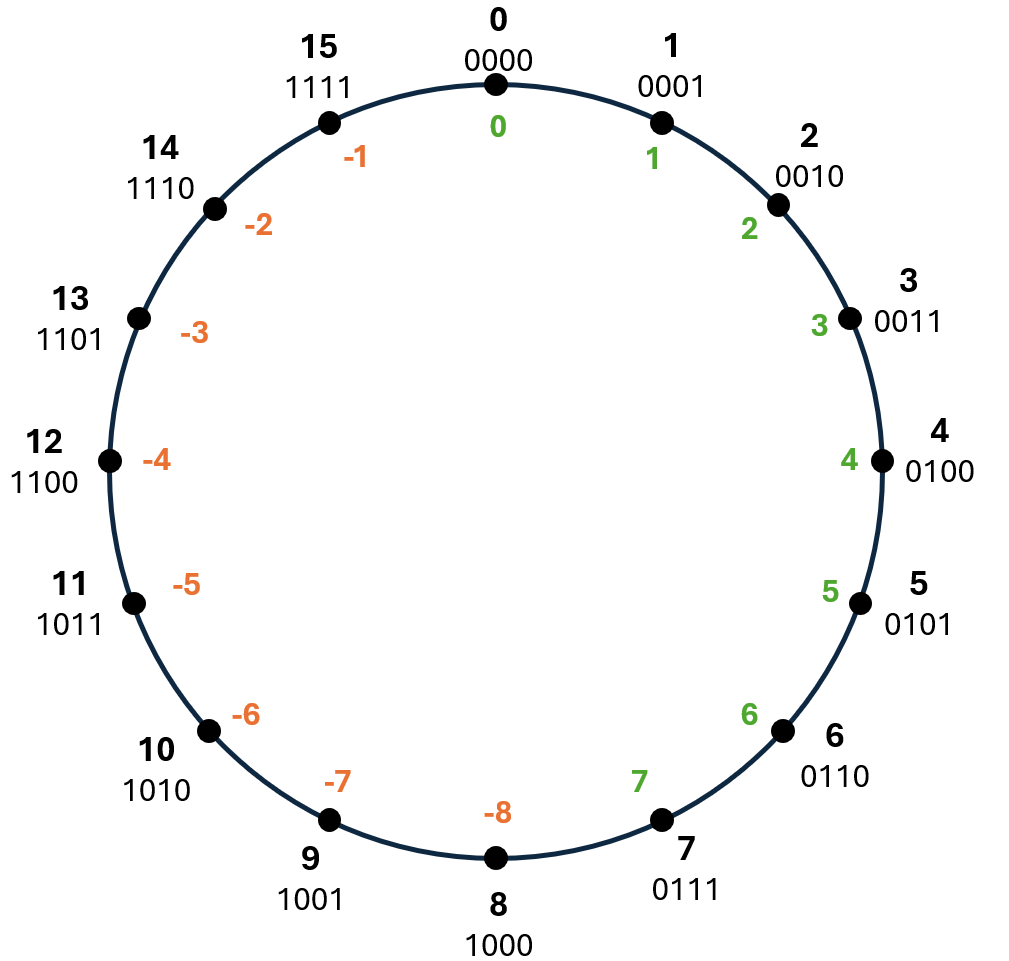
Der Binärkreis ist eine visuelle Methode, um zu verstehen, wie Computer negative Zahlen im Binärsystem darstellen. Er veranschaulicht das Konzept des Zweierkomplements.
Für eine feste Anzahl von Bits (z. B. 4 Bits) werden alle möglichen Binärzahlen in einem Kreis angeordnet.
Die erste Hälfte des Kreises repräsentiert die positiven Zahlen und die Null.
Bei 4 Bits sind das die Zahlen von 0000 (0) bis 0111 (7).
Die zweite Hälfte des Kreises, beginnend mit der höchsten negativen Ziffer (1000), repräsentiert die negativen Zahlen.
Bei 4 Bits sind das die Zahlen von 1000 (-8) bis 1111 (-1).
Eine Rechnung kann auf dem Binärkreis als eine Bewegung im Uhrzeigersinn (Addition) oder gegen den Uhrzeigersinn (Subtraktion) visualisiert werden. Bei dem Beispiel 5−6 startet man bei der Zahl 5 (0101) und bewegt sich 6 Schritte gegen den Uhrzeigersinn. Man landet bei 1111, was im Zweierkomplement der Dezimalzahl -1 entspricht.
Der Binärkreis macht sichtbar, dass die Addition und Subtraktion sich in diesem System in einem Kreislauf vollziehen.
