1.Grundlagen
Sprachen dienen als Grundlage für Kommunikation. Das kennen wir alle aus unserem Alltag. So kommunizieren beispielsweise Menschen untereinander mit Hilfe von natürlichen Sprachen, wie Deutsch und Englisch, oder auch durch Formelsprachen, wenn wir beispielsweise an die Physik oder Mathematik denken. Auch in der Informatik wird kommuniziert, und zwar nicht nur zwischen Mensch und Maschine durch Programmiersprachen, Kommandobefehle und ähnliches, sondern auch die Maschinen untereinander kommunizieren beispielsweise über Protokolle. Damit die Maschinen die verschiedenen Daten, die sie von außen bekommen verarbeiten können, benötigen sie formale Sprachen. Dazu zählen im speziellen Programmiersprachen, wie Java, Python oder Delphi, aber auch HTML und SQL.
1.1 Syntax und Semantik
Formale Sprachen sind also für die Kommunikation zwischen Maschinen notwendig. Nun soll ist es interessant deren innere Struktur und Bedeutung zu verstehen.
Jede formale Sprache ist durch ein striktes Regelwerk definiert, das bestimmt, welche Zeichenfolgen zulässig sind und welche Bedeutung diesen Zeichenfolgen zugewiesen wird.
Syntax:
Die Syntax entspricht den grammatikalischen Regeln einer Sprache. Es ist klar definiert, welche Wörter zur Sprache gehören und welche nicht.
Semantik:
Bei der Semantik geht es um den Inhalt bzw. die Bedeutung der notierten Wörter.
Durch die gegebene Syntax ist genau definiert, welche Ausdrücke zulässig sind und was durch diese geschehen soll. Dies erkennt man beispielsweise beim Programmieren, wenn ein Fehler angezeigt wird, weil ein Befehl nicht erkannt wurde. Die Syntax ist nicht korrekt und wir bekommen eine Fehlermeldung. In Python sieht das beispielsweise wie folgt aus:
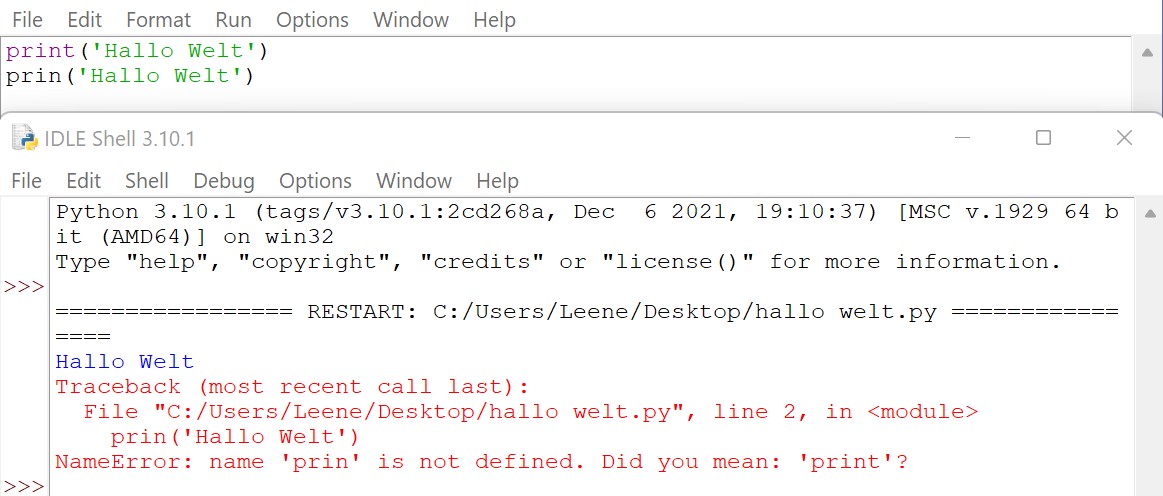
Nachfolgend nun ein praktisches Beispiel zur Unterscheidung von Syntax und Semantik:
Fruit flies like bananas.
Je nachdem, wie man den Satz liest, welche Grammatik man also zugrunde legt, kommt man auf zwei verschiedene Bedeutungsmöglichkeiten.
Aufgabe:
Auf welche zwei verschiedenen Arten kann man den Satz übersetzen und verstehen?


Die Syntax spielt hier eine entscheidende Rolle für die semantische Bedeutung.
Zwei weitere Beispiele wären:
- Paul sah den Mann auf dem Hügel mit dem Teleskop.
- Öffne die Kiste mit dem Schlüssel.
Aufgabe 1:
Überlege dir ein syntaktisch korrektes, aber semantisch sinnfreies Beispiel in Form eines kurzen Quelltextes.
Lösung
Beispiele: Endlosschleifen, sinnfreie bedingte Anweisungen (für Fälle die unmöglich sind)
Aufgabe 2:
Lies dir die folgenden Sätze durch. Jeder Satz ist grammatikalisch korrekt, hat also eine korrekte Syntax. Bewerte nun, ob der Satz auch semantisch korrekt ist. Wenn nicht, erkläre, warum der Satz zwar syntaktisch korrekt, aber semantisch falsch ist.
- Der Computer schläft unter der Lampe.
- Der Himmel ist blau, weil die Sonne scheint.
- Der Würfel ist rund.
Lösung
- Semantisch falsch: Ein Computer kann nicht schlafen und nicht unter einer Lampe liegen. Es fehlt die logische Bedeutung.
- Semantisch korrekt: Dieser Satz ist logisch nachvollziehbar, da der blaue Himmel durch die Streuung des Sonnenlichts erklärt wird.
- Semantisch falsch: Ein Würfel ist per Definition nicht rund. Die Begriffe widersprechen sich logisch.
Aufgabe 3:

Stell dir vor du arbeitest als Koch und hast ein Rezept für einen Kuchen bekommen. Dein Assistent hat das Rezept nach den Regeln der Sprache syntaktisch richtig aufgeschrieben, aber der Kuchen ist am Ende ungenießbar.
- Erkläre, warum dieses Rezept syntaktisch korrekt ist.
- Beschreibe, warum es semantisch fehlerhaft ist.
- Übertrage dieses Beispiel auf die Informatik. Welche Konsequenz hätte ein solch fehlerhaftes "Rezept" (Quellcode) für einen Computer?
Lösung
- Die Anweisungen sind in der deutschen Sprache korrekt formuliert.
- Die Zutaten sind logisch unsinnig für einen Kuchenrezept. Zucker und Salz wurden vertauscht und die Zutat Essig statt Milch ergibt keinen Sinn. Auch die Backzeit ist für einen Kuchen viel zu lang.
- Ein syntaktisch korrekter, aber semantisch fehlerhafter Code führt zu unerwarteten Ergebnissen. Ein Programm würde fehlerfrei kompilieren und starten, aber das Ergebnis wäre unsinnig. Das Programm "funktioniert" also, aber es erfüllt seine Aufgabe nicht.
1.2 Alphabet, Wort, Sprache
Als Grundlage für eine Grammatik wird ein Alphabet benötigt, mit dessen Hilfe Wörter einer Sprache formuliert werden können.
Alphabet
eine Menge von Zeichen bzw. Symbolen.
Wort
eine aus dem Alphabet gebildete endliche Zeichenkette.
Sprache
eine bestimmte Teilmenge von möglichen Wörtern über einem Alphabet. Deren Bildungsvorschrift entspricht einer Grammatik.
Nehmen wir als Beispiel-Alphabet ∑={h,n,u}. Daraus können nun verschiedene Worte gebildet werden wie zum Beispiel ω1=‘huhn‘, ω2=‘uhu‘ oder ω3=‘hnnhnn‘. Dabei spielt es keine Rolle, ob die Zusammensetzung der Zeichen ein semantisch korrektes Wort ergeben.
Eine Konkrete Sprache über diesem Alphabet könnten sein
L1={alle Wörter über ∑, die aus drei Buchstaben bestehen}.
Damit lassen sich alle Wörter dieser Sprache aufzählen. In diesem Fall wären das 33 =27 mögliche Wörter.
L={hhh, nnn, uuu, hhn, hhu, hnn, huu, hnu, hun, huh, hnh, nnh, nnu, nhh, nuu, nhn, nun, nuh, nhu, uun, uuh, unn, uhh, unu, unh, uhn, uhu}
Aufgabe 1:
Notiere ein syntaktisch korrektes, aber semantisch sinnfreies Beispiel in Form eines kurzen Quelltextes.
Lösung
BeispieL:
for (let i = 0; i < 10; i--) {
console.log("Dies ist ein Beispiel.");
Syntaktisch korrekt, da das Programm kompiliert und ausgeführt werden kann.
Semantisch sinnfrei, da eine Endlosschleife erzeugt wird.
}
Aufgabe 2:
Gegeben ist das Alphabet ∑={0,1}, sowie die Sprachen L1={|w|=2} und L2={w endet mit 0, |w|≤4}. Gib für beide Sprachen alle möglichen Wörter an.
Lösung
L1={00,01,10,11}
L2={0, 00, 10, 000, 010, 100, 110, 0000, 0010, 0100, 0110, 1000, 1010, 1100, 1110 }
Aufgabe 3:
Gegeben ist die Sprache L={ anbncn} über dem Alphabet ∑={a,b,c}, wobei n eine natürliche Zahl repräsentiert.
Welche der folgenden Worte gehören zur Sprache? Begründe kurz.
- aabbcc
- abbc
- abc
- cba
- AABBCC
- abcabc
Lösung
- gehört zur Sprache
- gehört nicht zur Sprache, da unterschiedliche Anzahlen von a, b und c
- gehört zur Sprache
- gehört nicht zur Sprache, da die Reihenfolge nicht stimmt
- gehört nicht zur Sprache, da die Zeichen nicht zum Alphabet gehören
- gehört nicht zur Sprache, da die Reihenfolge nicht stimmt.
Aufgabe 4:
