3. Automaten
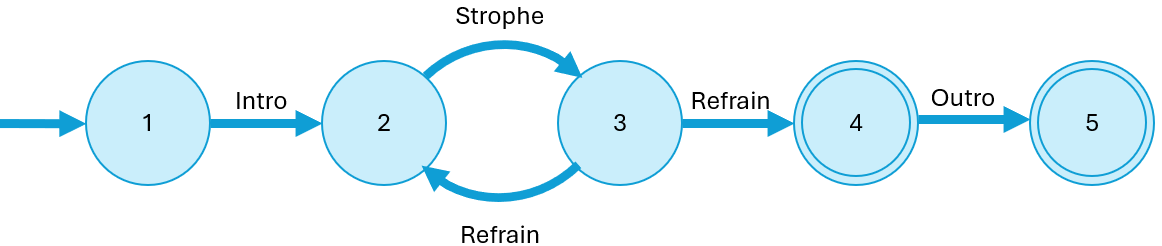
Stellt man sich ein Musikstück wie eine kleine Reise vor, so entsteht schnell ein Bild: Es gibt einen Anfang, Abschnitte mit Strophen und Refrains und schließlich ein Ende. Genau ein solches Bild vermittelt der "Liedautomat". Er beginnt mit dem Intro, gelangt durch eine Strophe in den nächsten Abschnitt und entscheidet sich beim Refrain, ob er zurückkehrt oder in eine neue Richtung weitergeht. Schließlich findet das Lied durch einen Refrain oder ein Outro seinen Abschluss.
Dieses Modell macht deutlich, dass Abläufe nicht zufällig entstehen, sondern sich durch eine feste Struktur beschreiben lassen. Jeder Schritt führt zu einem bestimmten Zustand, und nur bestimmte Übergänge sind möglich. Statt das Lied als Ganzes zu betrachten, wird es damit in klar unterscheidbare Stationen zerlegt.
Genau diese Idee steckt hinter Automaten: Sie sind Werkzeuge, um Prozesse, Abläufe und Eingaben systematisch zu beschreiben. Wie bei einem Stück Musik spielen feste Regeln eine Rolle, auf deren Grundlage ein Automat entscheidet, wohin die „Reise“ als Nächstes geht. Automaten verbinden so die zuvor erarbeiteten Konzepte zu formalen Sprachen und Grammatiken mit technischen Systemen– von einfachen Steuerungen bis hin zu komplexen Programmen.
3.1 verschiedene Arten von Automaten
Der Automat konsumiert Abschnitt um Abschnitt..
Wenn die Eingabe (in diesem Falle das Lied) vollständig konsumiert ist, gibt es zwei Möglichkeiten:
- der aktuelle Zustand ist ein Endzustand (markiert durch zwei Kreise) und die Eingabe wird akzeptiert.
- der aktuelle Zustand ist kein Endzustand und die Eingabe wird nicht akzeptiert.
Kommt ein Automat nicht weiter, weil kein Übergang zum aktuellen Eingabezeichen passt, wird die Eingabe ebenfalls nicht akzeptiert.
Enthält unser Lied beispielsweise noch eine Bridge vor dem Outro, kann der Automat dies nicht verarbeiten und stoppt ohne zu akzeptieren.
Ein Akzeptor ist ein spezieller endlicher Automat, der dazu dient, Wörter einer formalen Sprache zu erkennen, indem er sie entweder akzeptiert oder verwirft.
Aufgabe 1: Akzeptiert der Automat das Wort?
Wort: abba
Nun soll genauer betrachtet werden, wie diese Akzeptoren formal beschrieben werden können. Zwei zentrale Modelle bilden dabei die sogenannten endlichen Automaten.
Ein deterministischer endlicher Automat (DFA) zeichnet sich dadurch aus, dass er für jedes Eingabesymbol höchstens eine eindeutig festgelegte Übergangsmöglichkeit besitzt. Es ist also keine Auswahl verschiedener Wege möglich. Damit ist der Ablauf eines DFAs vollständig bestimmt.
Im Gegensatz dazu erlaubt ein nichtdeterministischer endlicher Automat (NFA) mehrere mögliche Übergänge für ein Eingabesymbol oder auch Übergänge ohne den Verbrauch eines Symbols (ε-Übergänge). Damit können NFAs flexibler beschrieben werden, was insbesondere beim Entwurf und bei der theoretischen Analyse von Sprachen Vorteile bringt.
Im Folgenden wird der Schwerpunkt auf NFAs gelegt, da sie oft eine einfachere Darstellung für viele Sprachen ermöglichen.
| nichtdeterministischer endlicher Automat | deterministischer endlicher Automat |
|---|---|
| nicht eindeutig → kann mit dem gleichen Zeichen in verschiedene Zustände wechseln | immer eindeutig → keine Auswahl verschiedener Wege möglich |
| leere Übergänge (ε) möglich | kein (ε) möglich |
Beispiele:
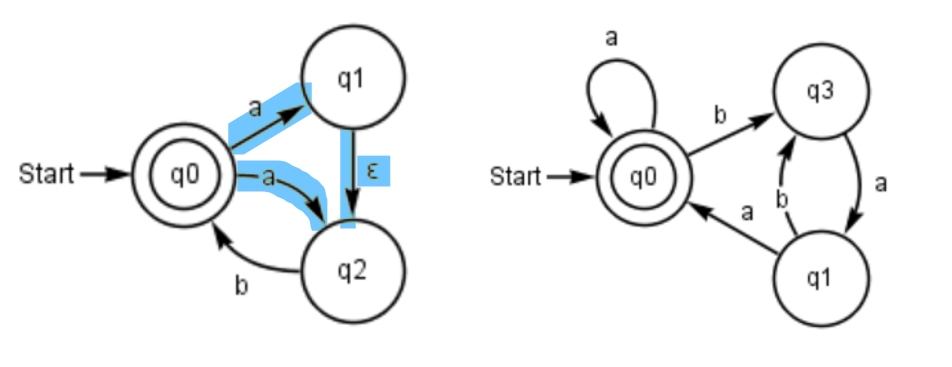
Aufgabe 1: Akzeptierte Sprache
Welche Sprache akzeptiert der Automat?
Welche Sprache akzeptiert dieser Automat?
Aufgabe 2: Automaten entwerfen
! Achtung! Hier ist etwas Frustrationstolleranz gefragt.
Lade dir das Programm
Exorciser.jar
herunter (Achtung! Externer Link!), wähle "Reguläre Ausdrücke in endliche Automaten überführen" und wähle als Schwierigkeit "Anfänger" aus.
Überlege dir:
Kann das Wort auch leer sein? Wenn ja -> Startzustand = Endzustand
Was ist das Minimum, dass ausgegeben werden muss?
Wählt man auf der Startseite des Exorcisers den Punkt "endliche Automaten in reguläre Ausdrücke überführen" kann das ganze auch umgekehrt geübt werden.
Aufgabe 3: praxisnahe Aufgabe
Viele Smartphones lassen sich außer per FaceID oder Fingerabdruck auch über einen PIN entsperren. Der Einfachheit halber wird angenommen, dass der PIN zweistellig sein muss.
Nur wenn die richtige PIN „42“ eingegeben wird, entsperrt sich das Handy. Jede andere Eingabe ist falsch und der Zugang wird verweigert.
Entwirf einen endlicher Automaten, der die Eingabe des PIN-Codes überprüft. Wird „42“ eingegeben, soll der Automat in einen akzeptierenden Endzustand gelangen.
Jede andere Eingabe führt in einen Fehlerzustand, der nicht akzeptierend ist.
Teste deinen Automaten mit folgenden Eingaben:
4 2
4 1
2 4
4 2 2
Lösung
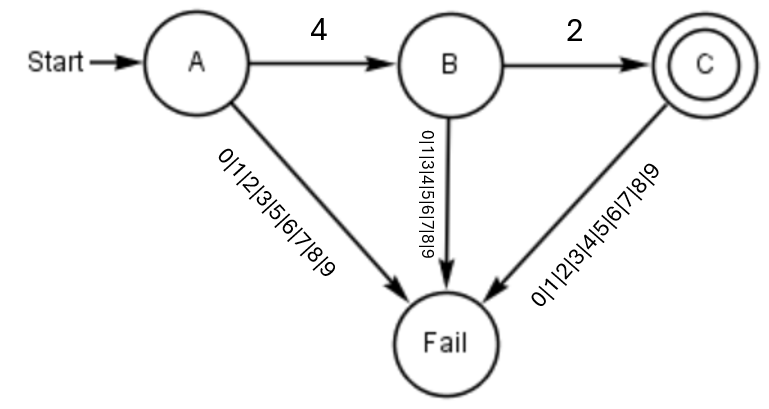
Wurde der Automat korrekt konstruiert, endet nur die erste Eingabe im Endzustand. Alle anderen Eingaben sollten im Fehler-Zustand landen.
Nachdem nun klar ist, was ein Automat ist und wie dieser aussehen kann, könnte man folgendes Gedankenexperiment durchführen:
Aufgabe:
Stell dir vor, einer deiner Mitschüler ist blind und du möchtest ihm erklären, wie so ein Automat aussieht.
Was muss alles angegeben bzw. beschrieben werden?
Es muss präzise angegeben werden, welche Zustände es gibt, welches Alphabet verwendet wird, welcher Zustand der Startzustand ist, welche Zustände Endzustände sind und schließlich wie die Übergänge definiert sind.
3.2 der Automat als 5-Tupel
Genau diese Aspekte lassen sich in einer formalen Struktur zusammenfassen. Ein endlicher Automat wird daher durch ein 5-Tupel beschrieben, das alle notwendigen Informationen enthält, um sein Verhalten eindeutig zu bestimmen.
Ein nichtdeterministischer, endlicher Automat M ist gegeben durch ein 5-Tupel, M=(Z,Σ,δ,Z0,E).
Dabei ist:
Z - endliche Menge an Zuständen
Σ - endliches Eingabealphabet (Zeichen des Alphabets und Zustände dürfen nicht die gleichen Namen haben)
δ - Überführungsfunktion (ordnet jedem Tupel aus Zustand und Eingabezeichen seine Folgezustände zu)
Z0 - Menge der Startzustände (Teilmenge von Z)
E - Menge der Endzustände (Teilmenge von Z)
So kann das 5-Tupel des Liedautomaten wie folgt angegeben werden:
M=(Z,Σ,δ,Z0,E)
Z={1, 2, 3, 4, 5}
Σ={Intro,Strophe,Refrain, Outro}
δ={ (1,Intro)=2, (2,Strophe)=3, (3,Refrain)=2, (3,Refrain)=4, (4,Outro)=5 }
Z0={1}
E={4,5}
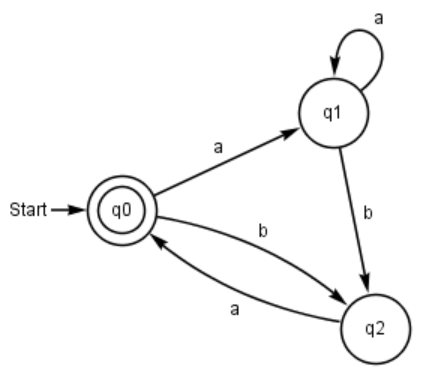
Aufgabe 1:
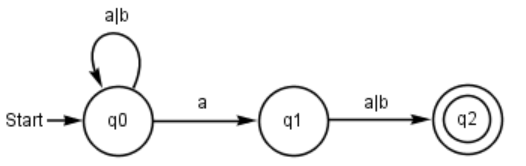
Gib das 5-Tupel des nebenstehenden Automaten an.
Lösung
M=(Z,Σ,δ,Z0,E)
Z={q0, q1, q2}
Σ={a,b}
δ={ (q0,a)=q0, (q0,b)=q0, (q0,a)=q1, (q1,a)=q2, (q1,b)=q2 }
Z0={q0}
E={q2}
Aufgabe 2:
- Notiere dir mindestens 3 aufeinanderfolgende Binärzahlen, die durch 4 teilbar sind. Erkennst du einen Zusammenhang?
- Konstruiere einen Automaten, der nur Binärzahlen akzeptiert, die durch 4 teilbar sind.
- Gib das 5-Tupel dieses Automaten an.
Lösung
- Alle durch 4 teilbaren Binärzahlen enden auf 00
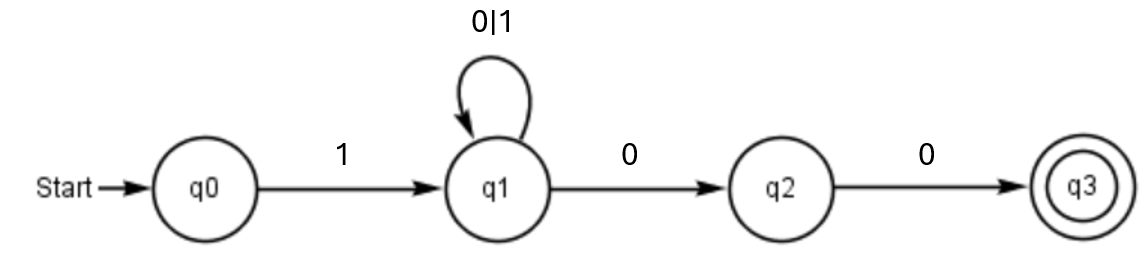
- M=(Z,Σ,δ,Z0,E)
Z={q0, q1, q2, q3}
Σ={0,1}
δ={ (q0,1)=q1, (q1,0)=q1, (q1,0)=q2, (q1,1)=q1, (q2,0)=q3 }
Z0={q0}
E={q3}
Aufgabe 3:
Zeichne den folgenden Automaten:
M=(Z, Σ,δ, Z0, E) mit
M=({z0, z1, z2, z3}, {'0','1'}, δ, {z0}, {z3})
δ= { (z0, 0)=z0, (z0,1)=z0, (z0, 1)=z1, (z1,1)=z2, (z2,0)=z3, (z3,0)=z3, (z3,1)=z3 }
Welche Sprache umfasst der Automat?
Lösung
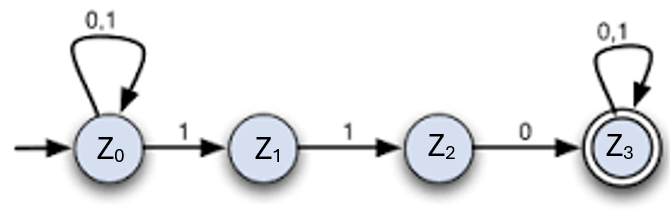Der Automat umfasst die Sprache aller Binärzahlen, die (an beliebiger Stelle) die Zeichenkette 110 enthalten.
3.3 Exkurs: Alan Turing und die Turingmaschine
Alan Turing gilt als einer der bedeutendsten Pioniere der Informatik. Bereits in den 1930er-Jahren entwickelte er mit der sogenannten Turingmaschine ein theoretisches Modell, das die Grundlagen moderner Computer bildet. Während des Zweiten Weltkriegs trug Turing durch die Entwicklung der Turingbombe, maßgeblich zur Entschlüsselung der deutschen Enigma-Codes bei, was den Kriegsverlauf entscheidend beeinflusste. Nach dem Krieg setzte er seine Forschung im Bereich der Computertechnik und der künstlichen Intelligenz fort und entwickelte den Turingtest. Damit legte er den Grundstein für viele heutige Technologien. Trotz seiner bahnbrechenden Leistungen blieb sein Leben von persönlichen und gesellschaftlichen Herausforderungen geprägt.
Bild von anthrowiki.at
Turings tragisches Leben
Alan Turing führte ein brillantes, aber zutiefst tragisches Leben. Er war Homosexuell und lebte heimlich mit seinem Freund zusammen, der sein Geheimnis verriet und ihn auslieferte. 1952 wurde er dann in Großbritannien wegen seiner Homosexualität strafrechtlich verfolgt, einer Zeit, in der diese noch als Straftat galt. Er musste sich zwischen Gefängnis und einer chemischen Kastration entscheiden und wählte die Hormonbehandlung. Diese schädigte nicht nur seinen Körper, sondern führte auch zu schweren Depressionen. Im Juni 1954 wurde Turing tot in seinem Haus aufgefunden mit einem vergifteten Apfel in seiner Hand. Es wird von einer selbst zugefügten Cyanidvergiftung ausgegangen – sein Tod gilt als Suizid. Wobei dies bis heute sehr umstitten ist. Erst Jahrzehnte später erfuhr er posthum Anerkennung für seine bahnbrechenden Leistungen, darunter die Entschlüsselung der Enigma-Codes im Zweiten Weltkrieg, die Millionen Menschenleben retteten. Dieses tragische Schicksal zeigt, wie gesellschaftliche Intoleranz einem der bedeutendsten Wissenschaftler des 20. Jahrhunderts das Leben kostete und wie wichtig es ist, Vorurteile zu überwinden.
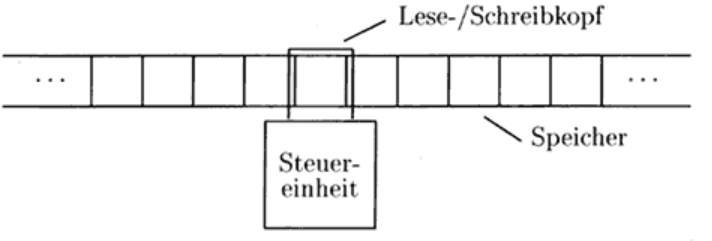
Die Turingmaschine ist ein theoretisches Modell eines Computers, das von Alan Turing entwickelt wurde. Ihr Kern besteht aus einem Band, das als Speicher dient und unendlich viele Felder enthält. Auf diesem Band liest und schreibt ein Lese-/Schreibkopf einzelne Zeichen aus einem festgelegten Alphabet.
Die Maschine arbeitet nach klar definierten Regeln: Je nach aktuellem Zustand und gelesenen Zeichen entscheidet die Steuerung, ob der Kopf das Zeichen verändert, in einen neuen Zustand wechselt und sich nach links oder rechts bewegt. Diese einfachen Schritte ermöglichen es, beliebige Berechnungen auszuführen und Algorithmen exakt zu beschreiben.
Mit diesem Konzept legte Turing den Grundstein für die moderne Informatik, da die Turingmaschine formalisierte, welche Aufgaben sich in der Theorie überhaupt von Computern lösen lassen und bildet dabei das zentrale Werkzeug zur Erforschung von Berechenbarkeit und Entscheidbarkeit.
Hier nochmal ein tolles Erklärvideo, welches sowohl die Turingmaschine beschreibt, als auch Turings tragisches Leben.
Die Turingmaschine ist eine verallgemeinerte Form des Automaten mit einem unbegrenzten Speicherband, auf dem sie lesen und schreiben kann. Dadurch ist sie wesentlich mächtiger als endliche Automaten oder Kellerautomaten. Während endliche Automaten nur bestimmte Sprachen (reguläre Sprachen) erkennen können, ist die Turingmaschine in der Lage, komplexere Berechnungen durchzuführen und damit Funktionen zu berechnen. Somit stellt die Turingmaschine das umfassendste und fundamentalste Modell in der Automatentheorie dar und bildet die theoretische Grundlage für das, was als berechenbar gilt
Wer so eine Turingmaschine gerne mal praktisch ausprobieren möchte kann sich zum Beispiel hier (Achtung! Externer Link) einen Simulator runterladen.
Nachdem Turingmaschinen als allgemeines Modell für Berechenbarkeit eingeführt wurden, stellt sich die Frage, welche Probleme sich mit ihnen lösen lassen – und welche nicht. Ein besonders wichtiges Beispiel dafür ist das Halteproblem. Dabei geht es um die Frage, ob man im Voraus entscheiden kann, ob eine Turingmaschine bei einer bestimmten Eingabe irgendwann stoppt – oder ob sie unendlich lange weiterläuft.
3.4 das Halteproblem
Stell dir vor, es gibt ein Computerprogramm. Man gibt diesem Programm eine Eingabe (z. B. eine Zahl oder einen Text), und das Programm führt daraufhin seine Befehle aus.
Jetzt stellt sich die Frage:
Kann man im Voraus immer sicher herausfinden, ob ein Programm irgendwann mit seiner Arbeit fertig wird – oder ob es für immer weiterläuft?
Genau darum geht es im Halteproblem:
Gesucht wäre ein „Überprüfungsprogramm“, das für jedes andere Programm und jede Eingabe zuverlässig entscheidet:
„Ja, dieses Programm hält irgendwann an.“
oder „Nein, dieses Programm läuft unendlich weiter.“
Die überraschende Erkenntnis der Informatik ist:
Ein solches allgemeines Überprüfungsprogramm kann nicht existieren. Für manche Programme lässt sich einfach nicht vorhersagen, ob sie anhalten oder ewig laufen.
Das Halteproblem ist also ein praktisch unlösbares Problem der Informatik.
Ein Alltagsbeispiel
Stell dir vor, du hast einen sehr fleißigen Roboter. Dieser Roboter kann Kochrezepte Schritt für Schritt abarbeiten. Du gibst ihm ein Rezept und er soll herausfinden, ob er irgendwann mit dem Kochen fertig wird oder ob er in einer Endlosschleife landet.
Warum das schwer ist:
Einfache Rezepte: Für viele Rezepte ist es leicht. "Nimm Brot, leg Käse drauf" – fertig. Der Rezept-Prüfer würde sagen: "Hält an."
Wiederholungen: "Rühre den Teig, bis er glatt ist." Das ist okay, irgendwann ist er glatt. Der Rezept-Prüfer könnte das erkennen.
Die kniffligen Fälle (Endlosschleife):
Stell dir vor, im Rezept steht: "Füge einen Löffel Salz hinzu. Wenn das Essen zu salzig schmeckt, entferne einen Löffel Salz. Wiederhole Schritt 1."
Was, wenn es nie zu salzig ist? Oder wenn es immer zu salzig ist und er immer Salz entfernt, das er vorher hinzugefügt hat?
Der Roboter könnte in einer Schleife festhängen: Salz hinzu, zu salzig, Salz weg, nicht zu salzig, Salz hinzu, zu salzig ... und so weiter.
Oder (mal abgesehen von den Rezepten): "Warte, bis die Ampel grün ist. Wenn die Ampel nicht grün ist, warte weiter."
Was, wenn die Ampel kaputt ist und nie wieder grün wird? Der Roboter würde für immer warten.
Die Unmöglichkeit:
Du kannst keinen Rezept-Prüfer bauen, der immer und für jedes beliebige Rezept garantieren kann, ob es jemals endet. Denn egal wie schlau dein Rezept-Prüfer ist, du könntest immer ein noch kniffligeres Rezept erfinden, das ihn austrickst und ihn dazu bringt, eine falsche Vorhersage zu machen oder selbst in einer Art Schleife zu landen, ohne eine Antwort zu finden.
Aufgabe: Endet die Zahlenfolge?
Es gibt ein Spiel mit Zahlen, das nach einer einfachen Regel funktioniert (bekannt als Kollatz-Folge):
Starte mit einer beliebigen positiven Zahl.
Wenn die Zahl gerade ist: Teile sie durch 2.
Wenn die Zahl ungerade ist: Multipliziere sie mit 3 und addiere 1.
Wiederhole die Regel mit der neuen Zahl.
Beispiel 6:
6 → 3 → 10 → 5 → 16 → 8 → 4 → 2 → 1
→ endet bei 1.
Spiele das Verfahren für die Startzahlen 7 und 12 durch und schreibe die Folge auf.
Überlege: Könnte es eine Zahl geben, bei der dieses Verfahren nie bei 1 ankommt, sondern unendlich weiterläuft?
Begründe deine Vermutung.
Lösung
7 → 22 → 11 → 34 → 17 → 52 → 26 → 13 → 40 → 20 → 10 → 5 → 16 → 8 → 4 → 2 → 1
12 → 6 → 3 → 10 → 5 → 16 → 8 → 4 → 2 → 1
Die Kollatz-Vermutung behauptet, dass die Folge immer irgendwann bei 1 ankommt – egal mit welcher Zahl man startet.
Aber bis heute weiß niemand sicher, ob das wirklich für alle Zahlen stimmt.
Kann KI das Haltproblem lösen?
Die einfache und leider auch enttäuschende Antwort ist: Nein, eine KI kann das Halteproblem prinzipiell nicht lösen.
Warum ist das so? Das liegt nicht daran, dass die KI nicht "schlau genug" ist oder noch nicht weit genug entwickelt wurde. Es ist ein grundlegendes, mathematisches Problem der Informatik, das unentscheidbar ist. Das wurde schon in den 1930er Jahren von Alan Turing bewiesen. Dieser Beweis gilt für jede Art von Computerprogramm, egal wie clever es ist. Eine KI ist am Ende auch "nur" ein sehr komplexes Computerprogramm.
Stell dir vor, du baust eine sehr kluge KI. Diese KI ist so programmiert, dass sie das Halteproblem löst. Sie nimmt also ein Programm X und eine Eingabe Y und sagt dir, ob X bei Y anhält oder nicht.
Jetzt kommt der Knackpunkt: Man könnte ein besonderes Programm Z basteln, das diese KI in einen Widerspruch führt. Dieses Programm Z könnte zum Beispiel so aussehen:
"Ich (Programm Z) nehme ein anderes Programm her. Dann frage ich die Halteproblem-KI, ob dieses andere Programm anhält. Wenn die KI sagt, das Programm würde anhalten, dann laufe ich (Z) in eine Endlosschleife. Wenn die KI sagt, das Programm würde nicht anhalten, dann stoppe ich (Z)."
Was passiert, wenn wir jetzt unsere eigene KI mit diesem Programm Z füttern und fragen, ob Z anhält?
Wenn die KI sagt: "Programm Z hält an" → Dann würde Z laut seiner eigenen Logik in eine Endlosschleife gehen. Das ist ein Widerspruch!
Wenn die KI sagt: "Programm Z hält nicht an" → Dann würde Z laut seiner eigenen Logik sofort anhalten. Auch das ist ein Widerspruch!
Dieses Gedankenexperiment zeigt, dass es unmöglich ist, eine solche KI (oder irgendein Programm) zu bauen, die immer korrekt entscheidet.
Was KIs aber können:
KIs können in vielen Fällen sehr gut raten oder heuristische Ansätze nutzen. Das heißt, eine KI könnte oft eine sehr gute Vermutung anstellen, ob ein Programm anhält oder nicht. Sie könnte es simulieren, Muster erkennen oder ähnliche Programme analysieren. Aber sie kann dir niemals eine 100%ige Garantie geben, dass ihre Antwort immer richtig ist. Für einige Programme und Eingaben würde sie einfach feststecken oder die falsche Antwort geben.
Fazit: Das Halteproblem ist eine fundamentale Grenze der Berechenbarkeit. Keine noch so fortschrittliche KI wird diese Grenze durchbrechen können, weil es ein logisches, nicht technisches Problem ist. Sie kann uns aber oft sehr gut dabei helfen, in der Praxis plausible Antworten zu finden, auch wenn sie keine absolute Sicherheit bieten kann.