4. Zusammenhang Automaten und Grammatiken
Wozu dienen Automaten im Kontext der formalen Sprachen und wie ist das bei Grammatiken?
Es existieren zwei unterschiedliche, aber gleichwertig wirkende Beschreibungsformen für bestimmte Sprachklassen: einerseits die regelbasierte Sicht über Grammatiken, andererseits die zustandsorientierte Sicht über Automaten. Im nächsten Schritt soll nun betrachtet werden, wie diese beiden Ansätze miteinander in Beziehung stehen.
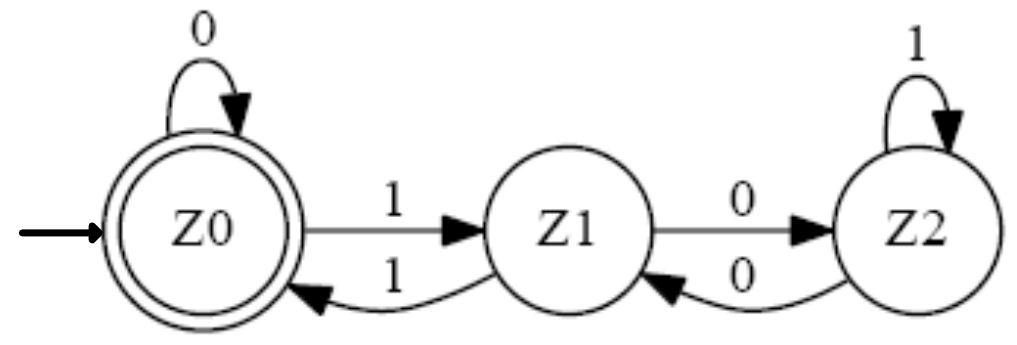
Der nebenstehende Automat kann, wie in Kapitel 2 von Automaten bereits erarbeitet, als 5-Tupel angegeben werden. Doch lässt sich zu diesem Automaten auch eine passende Grammatik aufstellen?
Ja! Es ist möglich mit Hilfe dieses Automaten eine dazu passende Grammatik anzugeben. Diese lautet wie folgt:
G=(N,T,P,S)
N= {Z0,Z1,Z2}
T= {0,1}
P= {Z0 → 0 Z0 | 1 Z1 | ε
Z1 → 1 Z0 | 0 Z2
Z2 → 1 Z2 | 0 Z1
}
S= Z0
Wichtig ist hierbei die Endzustände zu beachten. In diesem Beispiel reicht ein ε bei Zustand z0.
Anhand des Beispiels lässt sich feststellen, dass die Zustände und die Nichtterminale übereinstimmen. Selbiges gilt für das Eingabealphabet und die Terminale. Auch die Übergangsfunktion lässt sich mit Hilfe der Produktionsregeln darstellen. In obigem Beispiel klappt es auch mit dem Startsymbol und dem Startzustand.
Doch es stellt sich die Frage: Was ist, wenn der NFA mehrere Startzustände aufweist?
Eine Grammatik hat immer nur ein Startsymbol. Um diesen Unterschied auszugleichen, wird beim Überführen eines Automaten in eine Grammatik ein neuer künstlicher Startzustand eingeführt. Dieses Startsymbol erhält Produktionen, die unmittelbar mit Hilfe von ε-Übergängen zu den Nichtterminalen der ursprünglichen Startzustände führen. Auf diese Weise lassen sich mehrere Startzustände eines Automaten mit nur einem Startsymbol in der Grammatik darstellen.
Es lässt sich also aus jedem Automaten eine Grammatik ableiten.
Lässt sich aus der nachfolgenden Grammatik auch ein Automat ableiten?
G=(N,T,P,S)
N= {L,A}
T={a,b}
P={ L→aA ∣ bL ∣ a , A→bS ∣ a }
S= L
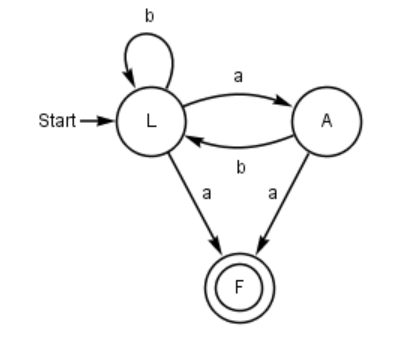
Beim konstruieren des Automaten kann festgestellt werden, dass die zwei gegebenen Nichtterminale als Zustände nicht ausreichen um den Automaten darzustellen. Es wird also ein weiterer Zustand benötigt.
In einer regulären Grammatik gibt es Regeln wie A→a. Das bedeutet: Vom Nichtterminal X kann direkt das Zeichen a erzeugt werden, und das Wort ist damit fertig.
Ein Automat funktioniert etwas anders: Er bleibt nach jedem gelesenen Zeichen in einem Zustand. Damit ein Wort, das mit einer solchen „abschließenden“ Regel endet, akzeptiert wird, braucht der Automat einen speziellen Endzustand.
Dieser Endzustand steht nicht für ein Nichtterminal aus der Grammatik, sondern zeigt nur an, dass ein Wort vollständig gelesen wurde. Deshalb hat der Automat meistens einen Zustand mehr als es Nichtterminale in der Grammatik gibt.
Zu jedem endlichen Automaten lässt sich eine äquivalente reguläre Grammatik konstruieren und umgekehrt.
Endliche Automaten und reguläre Grammatiken sind also äquivalent.
Aufgabe 1: Grammatik →Automat
Gegeben ist die Grammatik G=(N,T,P,S) mit
N= {S, A}
T= {a, b}
P= {S → aA | b, A → a}
S= S
Zeichne den passenden Automaten.
Lösung
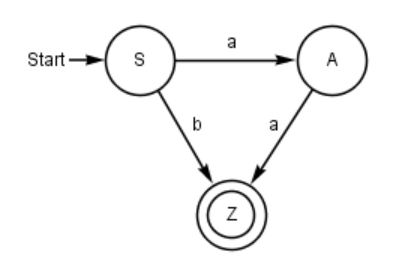
Es ist zu beachten, dass ein zusätzlicher Zustand als Endzustand eingefügt werden muss. Hier lässt sich im Unterrichtsgespräch gut hinterfragen, warum das notwendig ist.
Aufgabe 2: Grammatik ≠ Automat
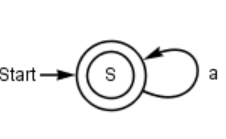
Eine Schülerin entwirft zu einer Grammatik mit der Produktionsregel P= {S → aS | a} den nebenstehenden Automaten.
Erkläre warum Grammatik und Automat nicht äquivalent sind.
Verbessere den Automaten, so dass eine Äquivalenz besteht.
Lösung
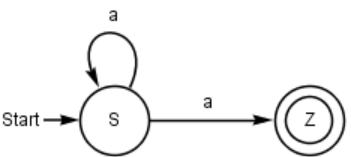
Durch den oben dargestellten Automaten würde auch das leere Wort akzeptiert werden, welches jedoch nicht von der Grammatik akzeptiert wird. Entsprechend darf der Startzustand nicht der Endzustand sein und es muss ein weiterer Zustand hinzugefügt werden, der durch ein 'a' erreicht werden kann.
Aufgabe 3: Automat → Grammatik

Gegeben ist nebenstehender Automatik.
Formuliere eine äquivalente Grammatik zu dem Automaten.
Welche Wörter werden von Automat bzw. Grammatik akzeptiert?
Lösung
G=(N,T,P,S)
N= {S, A, F}
T= {a, b}
P= {S → aA; A → b | bF; F → b | bF }
S= S
Alternativ kann auch auf das einzelne 'b' in den Produktionen verzichtet werden und F → ε ergänzt werden.
L=abn, n ≥ 1
Aufgabe 4: Automat und Grammatik erstellen
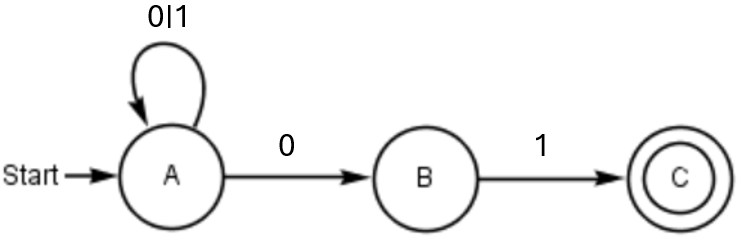
Erstelle eine Grammatik und einen Automaten, die die Sprache L={Binärzahlen, die auf 01 enden} akzeptieren.
Lösung
G=(N,T,P,S)
N={A, B}
T={0, 1}
P={A → 0A | 1A | 0B; B → 1}
S= S
Da von C kein Pfeil ausgeht, findet dieser in der Grammatik keine Beachtung.
