2. Die Grammatik
Nachdem die Grundlagen einer formalen Sprache – wie die Menge der gültigen Zeichen (Alphabet) und die Bedeutung von Wörtern (Semantik) – geklärt sind, stellt sich die Frage, wie sich aus diesen Elementen korrekte Sätze bilden lassen. Die Antwort auf diese Frage liefert die Grammatik. Sie dient als ein formales Regelwerk, das exakt festlegt, welche Kombinationen von Wörtern oder Zeichenfolgen als syntaktisch korrekt gelten und somit zur Sprache gehören. Die Grammatik ist damit das Herzstück, das die Struktur einer formalen Sprache definiert.
2.1 Bestandteile
Manche Grammatiken lassen sich sehr einfach beschreiben, wie das vorherige Beispiel von L1 zeigt. Hier war es vollkommen ausreichend zu sagen, dass die Worte aus zwei Zeichen des Alphabets bestehen sollen. Solche verbalen Beschreibungen sind leider nicht immer so einfach anzugeben. Oftmals ist es einfacher mit Hilfe von Produktionsregeln zu arbeiten.
Geben an, wie man aus Zeichen des Alphabets Wörter einer Sprache bilden kann.
Ein Beispiel für Produktionsregeln:
Satz → S P O S → Er S → Sie P → mag P → spielt P → hört O → Volleyball O → Schwimmen O → MusikMit Hilfe dieser Regeln können jetzt verschiedene Sätze gebildet werden, nämlich 2∙3∙3=18 Stück.
Es wären Sätze möglich wie „Er spielt Volleyball“ oder „Sie mag schwimmen“ die semantisch durchaus sinnvoll sind. Allerdings ist es genauso möglich und syntaktisch korrekt semantisch sinnfreie Sätze zu bilden wie „Sie hört Volleyball“ oder „Er spielt Schwimmen“. Diese gehören genauso zur Sprache, die durch die oben genannten Produktionsregeln angegeben wird.
Produktionsregeln bestehen immer aus sogenannten Nichtterminalen und Terminalen. Nichtterminale in unserem Beispiel sind Satz, S, P und O. Diese sind im fertigen Wort nicht mehr enthalten und dienen nur dem Aufbau bzw. der Strukturierung. Ein besonderes Nichtterminal ist das Startsymbol. Es gibt den Beginn der Bildungsvorschrift an. Im obigen Beispiel ist es das Nichtterminal Satz.
Terminale sind die am Ende noch übrigbleibenden Bausteine eines Wortes. Sie können mit anderen Terminalen kombiniert werden. Im obigen Beispiel sind das Er, Sie, mag, spielt, hört, Volleyball, Schwimmen und Musik.
Nichtterminale
kommen im fertigen Wort selbst nicht vor. Sie dienen der Beschreibung der Struktur eines Satzes.
Terminale
sind lexikalische Bausteine eines Wortes, die miteinander verbunden werden können.
Startsymbol
ist das Nichtterminal, mit dem die Bildung eines Wortes beginnt.
Sollen Produktionsregeln für eine Sprache angegeben werden, so gibt es dafür verschiedene Möglichkeiten. Es gibt also meist nicht nur eine richtige Lösung. Demnach sind alle nachfolgenden Produktionsregeln immer nur Beispiele für die entsprechende Sprache.
Aufgabe 1:
Notiere die Produktionsregeln für eine Sprache, ...
- mit der alle durch 5 teilbaren Zahlen kleiner als 1000 dargestellt werden können.
- für Geldbeträge in Euro, die kleiner sind als 100€.
- für alle geraden ganzen Zahlen kleiner als 5000.
Lösung
Die Schüler kennen den | Strich noch nicht. Sie müssten alle Regeln einzeln aufschreiben. Das wird schnell nervig und ist eine sehr gute Begründung den | schon mal einzuführen und auf die EBNF hinzuweisen.
- Fünfer → ZifferOhne0 Ziffer 0oder5 | ZifferOhne0 0oder5 | 0oder5
ZifferOhne0 → 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
Ziffer → ZifferOhne0 | 0
0oder5 → 0 | 5 - Geld → ZifferOhne0 Ziffer Komma Ziffer Ziffer Euro | Ziffer Komma Ziffer Ziffer Euro
Komma → ,
Euro → € - geradeZ → ZifferKleiner5 Ziffer Ziffer Gerade | ZifferOhne0 Ziffer Gerade | ZifferOhne0 Gerade | Gerade
ZifferKleiner5 → 1 | 2 | 3 | 4
Gerade → 0 | 2 | 4 | 6 | 8
Aufgabe 2:
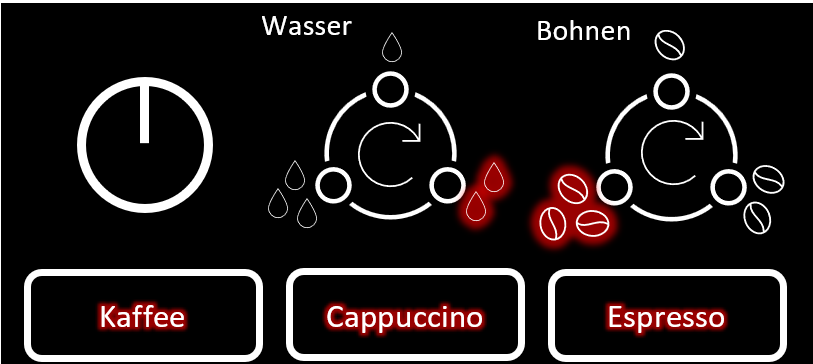
Ein mögliches Wort der Sprache von der nebenstehenden "Kaffeemaschine" könnte lauten:  Notiere zwei weitere mögliche Wörter der Sprache. Notiere die Produktionsregeln der Kaffeemaschine. |
|
Lösung
Lösungsansatz: NeedCoffee → Power Wasser Bohnen Sorte
2.2 das 4-Tupel
Für jede beliebige Sprache lässt sich eine Grammatik aufstellen. Diese hat folgenden Aufbau:
G=(N,T,P,S) ist ein vier-Tupel, wobei gilt:
N - endliche Menge der Nichtterminale
T – endliche Menge an Terminalen (N ∩ T=∅, d.h. es darf keine gleiche Benennung zwischen Terminalen und Nichtterminalen geben.)
P – endliche Menge an Produktionsregeln
S – Startsymbol (muss ein Element von N sein)
n 4-Tupel bedeutet, dass es eine geordnete Menge (immer die gleiche Reihenfolge) ist, die aus vier Elementen besteht.
Für das Beispiel der Kaffeemaschine könnte unsere Grammatik wie folgt aussehen:

Entwickelt man selbst eine Grammatik, ist es sinnvoll zuerst die Produktionsregeln zu notieren, um daraus dann die benötigten Terminale, Nichtterminale und das Startsymbol ablesen zu können.
Grammatiken können unterteilt werden nach der Chomsky-Hierarchie. Diese unterscheidet in Typ 0 (rekursiv aufzählbar), 1 (kontextsensitiv), 2 (kontextfrei) und 3 (regulär). Es gibt sogar Sprachen, die nicht vom Typ 0 sind und damit nicht von einer Grammatik dargestellt werden können.
Typ 3: Reguläre Grammatiken
Diese sind die einfachsten Grammatiken und können durch endliche Automaten verarbeitet werden. Sie erzeugen Sprachen, die als reguläre Sprachen bezeichnet werden. Ihre Regeln sind sehr restriktiv, da sie nur die Ersetzung eines Nichtterminalsymbols durch ein Terminalsymbol und optional ein weiteres Nichtterminalsymbol am Anfang oder Ende erlauben (z. B. A → aB oder A → a). Ein Beispiel ist die Sprache aller gültigen E-Mail-Adressen.
Typ 2: Kontextfreie Grammatiken
Diese Grammatiken sind mächtiger als reguläre Grammatiken. Sie werden von Kellerautomaten erkannt und sind die Grundlage vieler Programmiersprachen. Die Regeln sind so aufgebaut, dass ein einziges Nichtterminalsymbol durch eine beliebige Zeichenfolge ersetzt werden kann, unabhängig von seinem Kontext (z. B. A → aBC). Ein Beispiel dafür ist die Syntax von arithmetischen Ausdrücken wie (3 + 5) * 2.
Typ 1: Kontextsensitive Grammatiken
Sie sind mächtiger als kontextfreie Grammatiken, aber immer noch schwächer als Typ 0. Sie werden von linear beschränkten Turingmaschinen erkannt. Hier hängt die Ersetzung eines Nichtterminalsymbols vom Kontext ab (z. B. aAb → aCb). Das bedeutet, eine Regel darf nur angewendet werden, wenn das Symbol von bestimmten anderen Symbolen umgeben ist.
Typ 0: Rekursiv aufzählbare Grammatiken
Dies sind die mächtigsten Grammatiken. Sie können von Turingmaschinen erkannt werden und beschreiben alle Sprachen, für die ein Algorithmus existiert, der eine Zeichenkette erzeugen kann. Sie haben keine Einschränkungen bei ihren Regeln (z. B. ABC → a oder aB → bCa). Dazu gehören alle formalen Sprachen, die von einem Computer verarbeitet werden können.
Aufgabe 1:
Gegeben ist die Grammatik G=(N,T,P,S) einer Sprache L mit
N={Start, J, K},
T={j, k, l, m},
P={Start→kJ, Start→jK, J→kJ, J→m, K→jK, K→l },
S=Start
Aus welchen Wörtern besteht die Sprache L? Gib die Menge an (Aufzählung aller möglicher Wörter) und wenn möglich eine verbale Beschreibung.
Lösung
L= {km, kkm, kkkm, ..., jl, jjl, jjjl, ...}
Die Wörter bestehen entweder aus beliebig vielen k's mit einem m am Ende oder aus beliebig vielen j's mit einem l am Ende.
Aufgabe 2:
Erstelle eine Grammatik für die Darstellung der natürlichen Zahlen < 1000.
Lösung
G=(N,T,P,S)
N= {ZifferOhne0, Ziffer, Zahl}
T= {0, ..., 9}
P= {Zahl → ZifferOhne0 Ziffer Ziffer | ZifferOhne0 Ziffer | Ziffer
ZifferOhne0 → 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
Ziffer → ZifferOhne0 | 0 }
S= Zahl
Aufgabe 3:
Erstelle eine Grammatik für die Sprache aller geraden Binärzahlen.
Lösung
Alle geraden Binärzahlen enden auf 0.
G=(N,T,P,S)
N= {Binärzahl, Stelle}
T= {0, 1}
P= {Binärzahl → Stelle 0; Stelle → Stelle 0 | Stelle 1 | 1 | 0}
S= Binärzahl
Aufgabe 4:
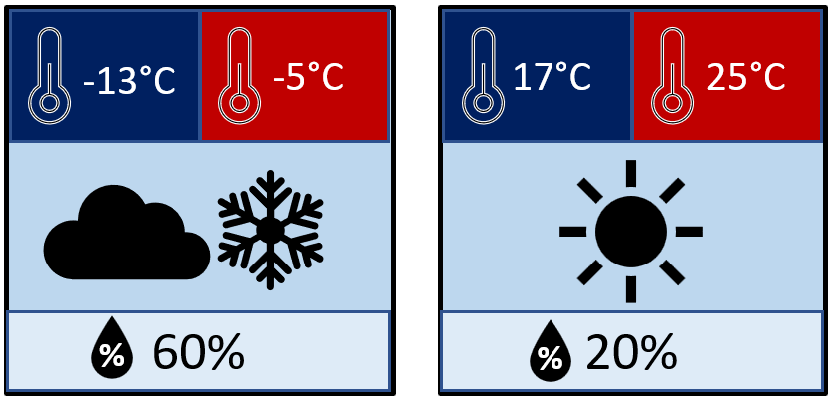
Erstelle eine Grammatik, die die Sprache der Wetterstation wiedergibt. Gib drei Beispiele für Wörter der Sprache an, von denen eins semantisch nicht korrekt ist.
Lösung
Alle Wörter bestehen aus einer Minimaltemperatur, einer Maximaltemperatur, einer "Wetterlage" und einer Luftfeuchtigkeit.
G=(N,T,P,S)
N= {Wetter, Temp, Wetterlage, Luftfeuchte, Symbol, Z1, Z2, Z3}
T= {°C, %, 0, …, 9, - }
P= {Wetter → Temp Temp Wetterlage Luftfeuchte;
Temp → - Z1 Z2 °C | Z1 Z2 °C | Z2 °C | - Z3 °C;
Z1 → 1 | 2 | 3 | 4 | 5 | 6; Z2 → 0 | Z3; Z3 → 1 | … | 9;
Wetterlage → Symbol | Symbol Symbol;
Symbol → Wind, Sonne, Wolken, Regen, Schnee, Gewitter;
Luftfeuchte → Z3 Z2 % | Z2 % }
S= Wetter
Semantisch nicht korrekt sind beispielsweise Wörter, deren Minimaltemperatur größer ist als die Maximaltemperatur oder die bei deutlich positiven Temperaturen Schnee vorhersagen.
2.3 Ableitungen
Ableitungen dienen dazu, zu zeigen, wie aus einem Startsymbol eine beliebige, gültige Zeichenkette (also ein Wort) einer Sprache erzeugt werden kann. Jede Ableitung ist eine schrittweise Anwendung der grammatikalischen Regeln, bis nur noch Terminalsymbole übrig sind.
Sie sind das grundlegende Werkzeug, um die Struktur und Zugehörigkeit von Wörtern zu einer Sprache nachzuweisen.
Die angewendeten Produktionsregeln werden, beginnend mit dem Startsymbol bis hin zum fertigen Wort, mit Hilfe von Pfeilen verdeutlicht.
Aussgehend von der angegebenen Grammatik würde eine Ableitung des Wortes -13°C -5°C Wolken Schnee 60% wie folgt aussehen:

Aufgabe 1:
Die Grammatik G = (N, T, P, S) einer Sprache L sei wie folgt definiert:
N = {Start, A, B}, T = {a, (, ), +, - *, /},
P = { Start→ Aa, Start→ A, A→ A-, A→ A+, A→ A*, A→ A/, A→ B, A→ A), A→ Aa, B→ (, B→ a }
S=S
Prüfe ob die folgenden Wörter Teil der Sprache sind. Begründe deine Entscheidung. Gib, falls möglich die Ableitung an.
- (a+a)/a
- )a-a/(
- a*a*(a-a)
- a/a
- (a+a)
- a-a*a
Lösung
- Start→ Aa → A/a → A)/a → Aa)/a → A+a)/a → Aa+a)/a → Ba+a)/a → (a+a)/a
- )a-a/( geht nicht, da am Anfang immer eine ( oder ein a stehen muss (da ein Ende nur durch ein B erreicht wird)
- Start → A → A) → Aa) → A-a) → Aa-a) → Ba-a) → (a-a) geht nicht, da vor einer ( nichts mehr kommen kann
- Start→ Aa → A/a → B/a → a/a
- Start → A → A) → Aa) → A+a) → Aa+a) → Ba+a) → (a+a)
- Start→ Aa → A*a → Aa*a → A-a*a → B-a*a → a-a*a
Aufgabe 2:
Gegeben ist eine Grammatik G=(N,T,P,S) für Binärzahlen mit N={A, B, C}, T={0,1}, S= A und
P= {A → ε, A→0A, A →1B, B→0C, B→1A, C→0B, C→1C }. Das Symbol ε entspricht dem leeren Wort. Es passiert also nichts. Prüfe für die Binärzahlen von 1 bis 15, ob sie sich mit Hilfe dieser Grammatik ableiten lassen. Entwickle Ideen, wie die obige Sprache in Worten beschrieben werden könnte.
Lösung
Die Sprache aller Binärzahlen, die durch 3 teilbar sind.
Abeiten lassen sich also die Zahlen 3, 6, 9, 12 und 15 bzw. 11, 110, 1001, 1100 und 1111.
2.4 die erweiterte Backus-Naur-Form
Nachfolgend sind zwei verschiedene Möglichkeiten für Produktionsregeln der Sprache der ganzen Zahlen dargestellt.
|
ganzeZahl → negZahl ganzeZahl → posZahl ganzeZahl → 0 negZahl → - posZahl posZahl → ZifferohneNull Ziffernfolge Ziffernfolge → Ziffer Ziffernfolge →Ziffernfolge Ziffer Ziffer → ZifferohneNull Ziffer → 0 ZifferohneNull →1 ZifferohneNull →2 ZifferohneNull →3 ZifferohneNull →4 ZifferohneNull →5 ZifferohneNull →6 ZifferohneNull →7 ZifferohneNull →8 ZifferohneNull →9 |
ganzeZahl → ‘0‘ | [‘-‘ ] ZifferohneNull {Ziffer} Ziffer → ZifferohneNull | ‘0‘ ZifferohneNull → ‘1‘ |‘2‘ | ‘3‘ | ‘4‘ | ‘5‘ | ‘6‘ | ‘7‘ | ‘8‘ | ‘9‘ |
Schon auf den ersten Blick fällt auf, dass die erste Variante deutlich umfangreicher und dadurch auch unübersichtlicher ist. Dafür sind in der zweiten Variante Anführungszeichen, Striche und verschiedene Klammern enthalten, die erstmal unklar sind. Hier wurde die so genannte erweiterte Backus-Naur-Form benutzt.
Die Backus-Naur-Form (BNF) wurde ursprünglich nach John Backus und Peter Naur, zwei Pioniere der Informatik, benannt. Sie entwickelten 1960 die Programmiersprache ALGOL 60. Ziel war es eine formal exakte Beschreibung der Syntax einer Programmiersprache anzugeben. Es sollten also keine Ungenauigkeiten durch natürliche Sprachen mehr enthalten sein. Es gibt viele Varianten der BNF. Die am häufigsten verwendete ist wohl die von Niklaus Wirth entwickelte erweiterte Backus-Naur-Form (EBNF). Dieser entwickelte sie ursprünglich für die syntaktische Darstellung der Programmiersprache Pascal. Die EBNF wurde von der ISO standardisiert (ISO/IEC 14977:1996(E)). Auch von ihr gibt es trotz dessen verschiedene Abwandlungen.
Die erweiterte Backus-Naur-Form ist eine Metasprache zur Darstellung von (kontextfreien) Grammatiken. Es gelten folgende Regeln:
‘…‘ Terminale werden in Anführungszeichen geschrieben.
… | … oder
(…) Gruppierungen
[…] Optional (etwas kommt einmal vor oder gar nicht)
{…} Wiederholung (etwas kommt beliebig oft oder gar nicht vor)
Nehmen wir uns die erste Zeile des obigen Beispiels zu den natürlichen Zahlen noch einmal her.
ganzeZahl → ‘0‘ | [‘-‘ ] ZifferohneNull {Ziffer}
Die Zahl ist entweder 0 oder wie folgt aufgebaut:
Am Anfang steht ein Minus (wenn es eine negative Zahl ist) oder nicht (positive Zahl). Darauf folgt eine Ziffer die nicht 0 ist. Die Zahl ist also mindestens einstellig. Anschließend kommen beliebig viele weitere Ziffern (zwischen 0 und 9).
Aufgabe 1:
Überprüfe ob die folgenden Worte mit Hilfe der entsprechenden EBNFs gebildet werden können:
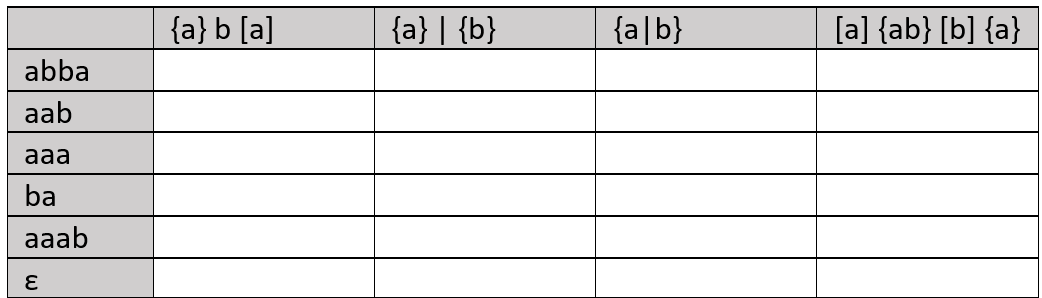
Lösung
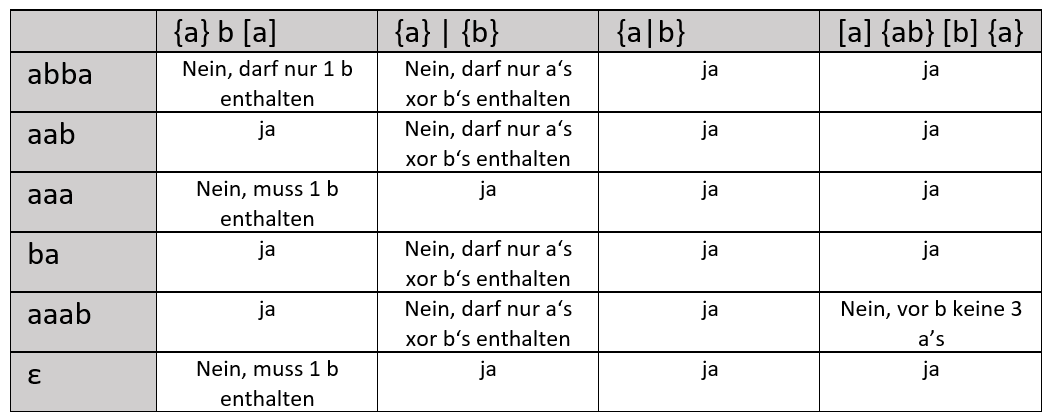
Aufgabe 2:
Führe den Test durch. (Achtung externer Link! Du verlässt hierfür die Seite des Lehrwerks.)
Aufgabe 3:
Zähle alle Worte auf, die mit Hilfe der nachfolgenden Produktionsregeln gebildet werden können. Das Startsymbol ist X.
X → (‘a‘ [Y]) | Z , Y → ‘b‘ ‘c‘ (‘b‘ | Z), Z → ‘d‘ ([‘e‘] | ‘f‘)
Lösung
X → a
X → a Y → a b c b oder a b c Z
a b c Z → a b c d oder a b c d e oder a b c d f
X → Z → d oder d e oder d f
Aufgabe 4:
Erstelle eine Grammatik zum Hausbau aus den nachfolgenden Vorgaben, Nutze hierfür die EBNF.
- Ein Haus besteht aus genau 4 Wänden, einer Haustür und einem Dach.
- In jeder Wand können beliebig viele Fenster enthalten sein.
- Außerdem kann es Innenwände und einen Garten haben.
- Das Dach besteht aus beliebig vielen Ziegeln, Dachfenstern und eventuell einem Schonstein.
- Ein Garten besteht aus einem Weg, beliebig vielen Blumen und eventuell einem Gemüsebeet.
Lösung
G=(N,T,P,S)
N= {Haus, W Dach, Garten }
T= {Tür, Innenwand, Wand, Fenster, Ziegel, Dachfenster, Schornstein, Weg, Blume, Gemüsebeet}
P= {Haus → W W W W Tür Dach {Innenwand} [Garten];
W → Wand {Fenster}
Dach → {Ziegel} {Dachfenster} [Schornstein]
Garten → Weg {Blume} [Gemüsebeet]}
S= Haus
Aufgabe 5:
Es gibt verschiedene Vorgaben, die für eine gültige E-Mail-Adresse erfüllt sein müssen. Einige sind nachfolgend aufgezählt:
- Links vom ‘@‘ steht ein Benutzername und rechts davon der Name der Internet-Domain
- Der Benutzername besteht aus mindestens einem Zeichen. Es dürfen Kleinbuchstaben, Ziffern, Binde-, Unterstriche, Punkte und Ausrufezeichen verwendet werden
- Die Internet-Domain besteht aus mindestens einer Unterdomain gefolgt von einer Top-Level-Domain wie de oder com.
- Zwischen zwei Domains steht ein Punkt
- Die Top-Level-Domain besteht aus zwei bis vier Buchstaben.
- Unterdomains bestehen aus mindestens zwei Zeichen. Diese können Buchstaben, Ziffern und Bindestriche sein, wobei Bindestriche nicht am Anfang oder am Ende stehen dürfen.
Lösung
G=(N,T,P,S)
N= {Mail, Benutzername, Domain, Z, Sub, Top, B, Ziffer}
T= {@,a ,..., z , 0 ,..., 9 , - , _ , . , ! }
P= {Mail → Benutzername @ Domain;
Benutzername → Z {Z};
Z → B | Ziffer | - | _ | . | ! ;
Domain → Sub {. Sub} . Top;
Top → B B [B] [B];
B → a |...| z;
Ziffer → 0 |...| 9;
Sub → (B | Ziffer) {B | Ziffer | -} (B | Ziffer);}
S= Mail
