3.1 Sequenz (Aufeinanderfolge)
Der Ablaufsteuerung der Python-Programme liegt stets die Kontrollstrukur Sequenz (Aufeinanderfolge) zugrunde.
In der Abbildung 1 ist die Kontrollstrukur Sequenz im Struktogramm dargestellt.
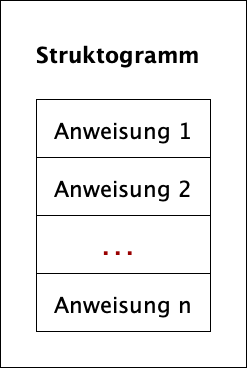
In der Abbildung 2 ist ein Algorithmus im Struktogramm dargestellt, der aus einer Sequenz von neun Anweisungen besteht.

Im Algorithmus werden die Volumina des Kreiszylinders, Kreiskegels und Kreiszylinders mit aufgesetztem Kreiskegel berechnet und ausgegeben. PI ist dabei die Konstante π zum Berechnen der Kreisfläche.
In den Abbildungen 3 und 4 sind ein Kreiszylinder und ein Kreiskegel dargestellt.


- Die Volumenformel des Zylinders lautet VZ=π⋅r2⋅h, wobei r der Radius des Grundkreises ist und h die Höhe des Zylinders.
- Die Volumenformel des Kegels lautet VK=1/3⋅π⋅r2⋅h, wobei r der Radius des Grundkreises ist und h die Höhe des Kegels.
- Die Volumenformel des Zylinders mit aufgesetztem Kegel lautet VZK=VZ+VK.
Programm »volumina1.py«
Das Programm – in dem der Algorithmus implementiert ist – besteht aus zwei Teilen.
- Der grafischen Benutzeroberfläche – dem Hauptfenster mit Label-, Entry- und Button-Widgets (Abbildung 5).
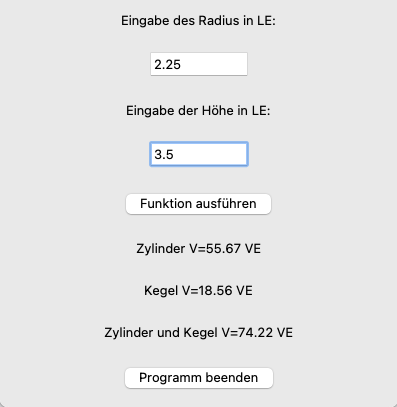
- Der Callback-Funktion »berechnen« mit dem Algorithmus (Abbildung 2).
import tkinter as tk
import math
# Callback-Funktion
def berechnen():
try:
radius=float(entry1.get())
hoehe=float(entry2.get())
grundflaeche=math.pi*radius**2
volumen1=grundflaeche*hoehe
volumen2=1/3*grundflaeche*hoehe
volumen3=volumen1+volumen2
label3.config(\
text=f"Zylinder V={volumen1:.2f} VE")
label4.config(\
text=f"Kegel V={volumen2:.2f} VE")
label5.config(\
text=f"Zylinder und Kegel V={volumen3:.2f} VE")
except ValueError:
label3.config(text="Falsche Eingabe(n)!")
entry1.delete(0, tk.END)
entry2.delete(0, tk.END)
# grafische Benutzeroberfläche
root=tk.Tk()
root.title("Volumina")
root.geometry("400x410")
root.resizable(False, False)
# Widgets
label1=tk.Label(root, text="Eingabe des Radius in LE:")
entry1=tk.Entry(root, width=10)
label2=tk.Label(root, text="Eingabe der Höhe in LE:")
entry2=tk.Entry(root, width=10)
button1=tk.Button(root, text="Funktion ausführen",\
command=berechnen)
label3=tk.Label(root, text="Zylinder V=")
label4=tk.Label(root, text="Kegel V=")
label5=tk.Label(root, text="Zylinder und Kegel V=")
button2=tk.Button(root, text="Programm beenden",\
command=root.destroy)
label1.pack(pady=10)
entry1.pack(pady=10)
label2.pack(pady=10)
entry2.pack(pady=10)
button1.pack(pady=10)
label3.pack(pady=10)
label4.pack(pady=10)
label5.pack(pady=10)
button2.pack(pady=10)
root.mainloop()
| 2. Zeile | Das Modul »math« wird wegen der Konstante »pi« in das Programm eingebunden. |
| 5. bis 22. Zeile | Die Callback-Funktion »berechnen« wird deklariert. |
| 6. bis 20. Zeile |
Durch »try« und »except« erfolgt eine Ausnahmebehandlung.
|
| 7. und 8. Zeile |
In den zwei Entry-Widgets erfolgen die Benutzereingaben der Werte für die Variablen »radius« und
»hoehe«
|
| 10., 11., 12. Zeile |
Das Volumen des:
|
| 13. bis 18. Zeile |
In drei Label-Widgets erfolgen die Ausgaben der Gleitkommawerte der Variablen »volumen1«,
»volumen2« und »volumen13« in f-Strings im numerischen Festkommaformat mit zwei
Nachkommastellen.
|
| 21. und 22. Zeile | Die Inhalte der Eingabefenster (Entry-Widgets) werden gelöscht. |
Variablen können Werte des Datentyps »float« zugewiesen werden. Die Werte werden Gleitkommazahlen genannt.
Wichtig zu wissen ist, dass die Anzahl der Gleitkommazahlen – im Unterschied zu den Dezimalzahlen in der Mathematik – nur endlich ist.
In der Abbildung 6 ist das Syntaxdiagramm für »Gleitkommazahl« in Festkommaformat und in der Abbildung 7 in Fließkommaformat dargestellt.
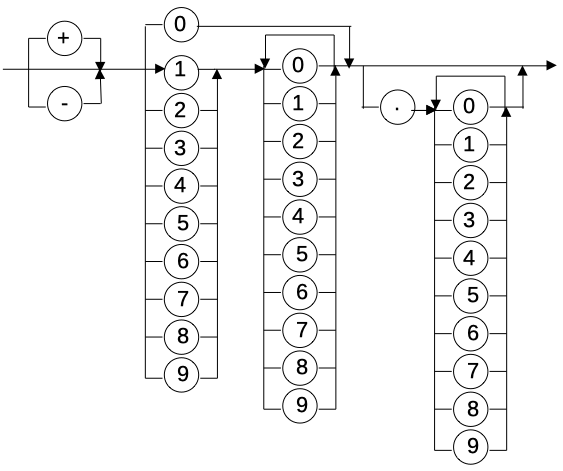
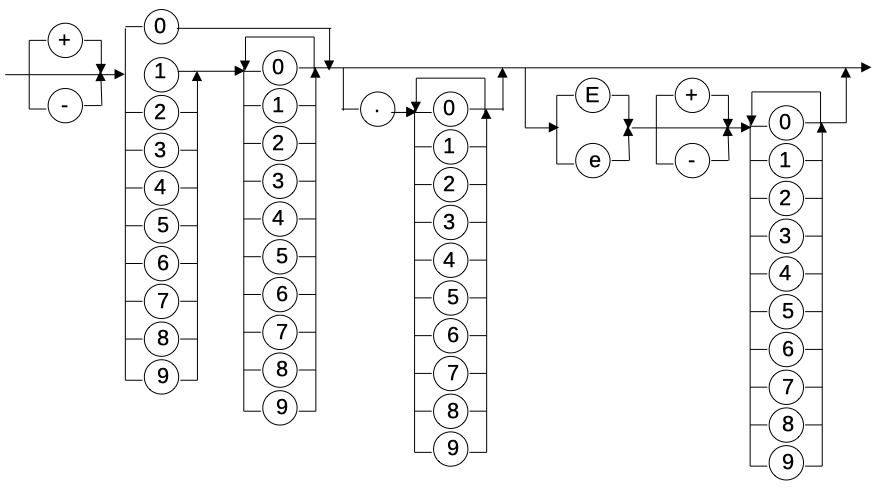
Beispiele für Gleitkommazahlen:
- -45.103, -0.2, 0.0 und +987.76 im Festkommaformat
- 1e3, -0.2e-2, 3.5E4 und 3.6e+1 im Fließkommaformat
Die Rechenoperationen mit Gleitkommazahlen sind:
- + Addition (7.2+5.9 → 13.1)
- - Subtraktion (1e2-34,12 → 65.88 )
- * Multiplikation (2.6*-1.7e-2 → -0.0442)
- / Division (123.9/30 → 4.13)
- // ganzzahlige Division (123.9//30 → 4)
- % Rest bei ganzzahliger Division (10.0%4.0 → 2.0)
- ** Potenzieren (1E2**2 → 10000.0)
Gleitkommazahlen sind keine Zeichenketten (Strings), deshalb ist bei den Ein- und Ausgaben von Gleitkommazahlen folgendes zu beachten:
-
Eine eingegebene Zeichenkette (String), die dem numerischen Format einer Gleitkommanzahl entspricht, wird mit
der Funktion »float()« in eine Gleikommazahl konvertiert.
Beispielsweise wird die Zeichenkette "1e2" durch float(1e2) in die Gleitkommazahl 100.0 konvertiert. -
Ausgegeben wird eine Gleitkommazahl, indem das numerische Format der Gleitkommazahl
in eine Zeichenkette (String) konvertiert wird.
Beispielsweise wird die Gleitkommazahl 1e2 duch den f-String f"{1e2}" in die Zeichenkette "100.0" konvertiert. -
Es ist sinnvoll, Gleitkommazahlen im Festkommaformat mit einer bestimmten Anzahl von Nachkommastellen
auszugeben.
Beispielsweise wird die Gleitkommazahl »math.pi« durch den f-String f"{math.pi:.2f}" in die Zeichenkette "3.14" konvertiert.
In Deutschland wird der ganze Teil einer Gleitkommazahl vom gebrochenen Teil durch ein Komma
getrennt (beispielsweise 4,5 und -100,0).
Dagegen wird in Python die englische Schreibweise verwendet. Das heißt, daß der ganze vom gebrochenen Teil
durch einen Punkt getrennt wird (beispielsweise 4.5 und 100.0).
Aufgabe A13
Gegeben ist der in der Abbildung 6 im Struktogramm dargestellte Algorithmus.

Im Algorithmus wird das Volumen eines Quaders, das Volumen einer Rechteckpyramide und das Volumen des Quaders mit der ihm aufgesetzten Rechteckpyramide berechnet und ausgegeben.
Implementiere ein Programm »volumina2.py« am Computer.
- Im Programm soll der Algorithmus in einer Callback-Funktion umgesetzt werden.
- Führe das Programm aus und teste, ob es fehlerfrei läuft und den gestellten Anforderungen entspricht.
