3.2.3 Lineare Gleichung
Die Gleichung a·x + b = 0 heißt lineare Gleichung, weil die Variable x in der ersten Potenz (x1) steht.
Lösen der linearen Gleichung a·x + b = 0
Gegben sind die Dezimalzahlen a und b. Zum Lösen der Gleichung a·x + b = 0 findet eine vollständige Fallunterscheidung statt:
- Falls a = 0 und b = 0 gilt, ist für x jede Dezimalzahl Lösung.
- Falls a = 0 und b ≠ 0 gilt, gibt es keine Lösung.
- Falls a ≠ 0 gilt, ist x = -b/a die Lösung.
Programm »gleichung.py«
Das Programm leistet das Folgende:
- (E) Eingebender Gleitkommazahlen a und b.
- (V) Verarbeitung, indem die lineare Gleichung a·x + b = 0 gelöst wird.
- (A) Die Lösung wird ausgegeben.
Zum Lösen der linearen Gleichung ist der in der Abbildung 1 dargestellte Algorithmus gegeben.
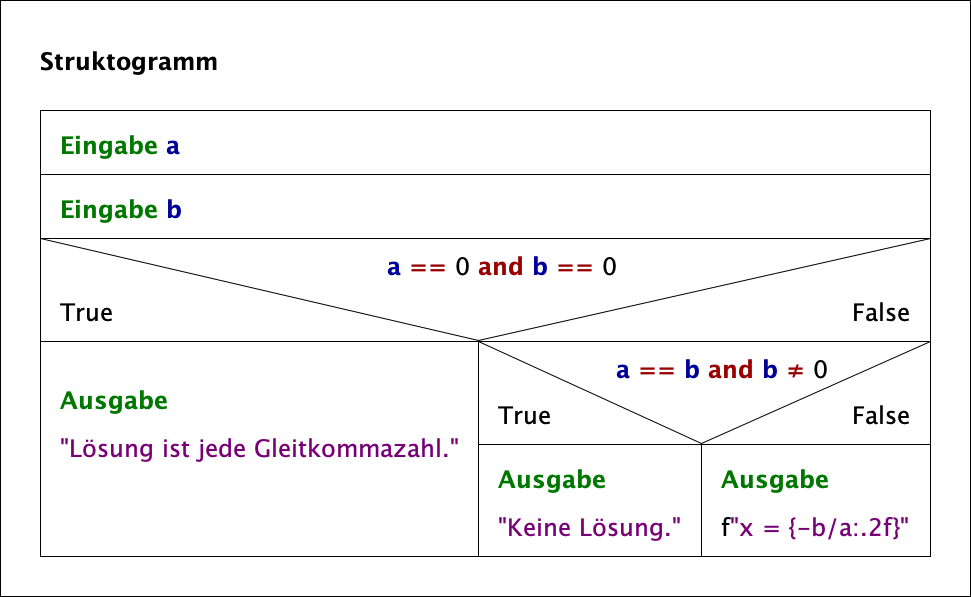
Nachfolgend ist der Quelltext des Programms mit der Callback-Funktion »loesen« und der grafischen Benutzeroberfläche – dem Hauptfenster mit Widgets – gegeben.
- Der Callback-Funktion »loesen« liegt der in der Abbildung 1 dargestellte Algorithmus zugrunde.
import tkinter as tk
# Callback-Funktion
def loesen():
try:
a=float(entry1.get())
b=float(entry2.get())
if a==0 and b==0:
label3.config(\
text="Lösung ist jede Gleitkommazahl.")
elif a==0 and b!=0:
label3.config(text="Keine Lösung.")
else:
label3.config(text=f"x={-b/a:.2f}")
except ValueError:
label3.config(text="Falsche Eingabe(n)!")
entry1.delete(0, tk.END)
entry2.delete(0, tk.END)
# grafische Benutzeroberfläche
root=tk.Tk()
root.title("Lineare Gleichung")
root.geometry("400x325")
root.resizable(False, False)
# Widgets
label1=tk.Label(root, text="Eingabe der Gleitkommazahl a")
entry1=tk.Entry(root, width=10)
label2=tk.Label(root, text="Eingabe der Gleitkommazahl b")
entry2=tk.Entry(root, width=10)
button1=tk.Button(root, text="Lösen", command=loesen)
label3=tk.Label(root, text="")
button2=tk.Button(root, text="Programm beenden!",\
command=root.destroy)
label1.pack(pady=10)
entry1.pack(pady=10)
label2.pack(pady=10)
entry2.pack(pady=10)
button1.pack(pady=10)
label3.pack(pady=10)
button2.pack(pady=10)
root.mainloop()
| 4. bis 18. Zeile | Die Callback-Funktion »loesen« wird deklariert. |
| 5. bis 16. Zeile | Die »,try« und »except« Ausnahmebehandlung der Eingaben erfolgt. |
| 6. und 7. Zeile | Den Variablen »a« und »b« werden die dem Eingabefeld eingegebenen Zeichenketten durch die Funktion »float()« (Typumwandlung) als Gleitkommazahlen zugewiesen. |
| 8. bis 14. Zeile |
Die if-elif-else-Anweisung ist eine mehrfache Auswahl (Selektion) mit drei Bedingungszweigen:
|
| 9., 10. und 12. Zeile | Ausgaben, die in Zeichenketten erfolgen. |
| 14. Zeile | Die Ausgabe der Lösung erfolgt im f-String »f"x={-b/a:.2f}"«.[1] |
| 20. Zeile | Eine Kommentarzeile, die im Programmablauf unberücksichtigt bleibt. |
Aufgabe A20
Implementiere das Programm »gleichung.py« am Computer.
Führe das Programm u. a. mit folgenden Eingaben aus und teste, ob es fehlerfrei läuft und den gestellten Anforderungen entspricht:
- a = 14 und b = 7
- a = 4.5 und b = -9
- a = 0 und b = 5.3
- a = -100.0 und b = 0
- a = 0 und b = 0
Vergleiche die Ausgaben des Programms mit deinen Lösungen aus der oben gestellten Aufgabe A19.
Aufgabe A21
Implementiere ein Programm »gleitkommazahlen.py« am Computer.
Das Programm soll das Folgende leisten:
- (E) Eingegeben werden sollen zwei Gleitkommazahlen.
- (V) Verglichen werden soll, ob die erste Zahl:
- kleiner als die zweite Zahl ist
- größer als die zweite Zahl ist
- gleich der zweiten Zahl ist
- (A) Ausgegeben werden soll das Ergebnis des jeweiligen Vergleichs.
Führe das Programm mit allen drei Fällen Eingaben aus und teste, ob es fehlerfrei läuft und den gestellten Anforderungen entspricht:
- [1]
Da jede Ausgabe auf dem Bildschirm des Computers eine Zeichenkette ist, wird die berechnete Zahl -b/a
im f-String f"x = {-b/a:.2f}" in Zeichen umgewandelt.
Zum Beispiel ergibt f"x = {-3/2:.2f}" als Ausgabe die Zeichenkette »x = -0.67« mit der Beschränkung auf zwei Nachkommastellen. Ohne die Beschränkung f"x = {-3/2}" auf Nachkommastellen würde »x = -0.6666666666666666" « ausgegeben werden.
