3.5 Iteration und Rekursion
Ein iterativ gelöstes Problem lässt sich rekursiv lösen und umgekehrt
Zum Vergleichen werden der iterative und rekursive Algorithmus zum Lösen des Problems der Summe der Ganzzahlen von 1 bis n>0 herangezogen.
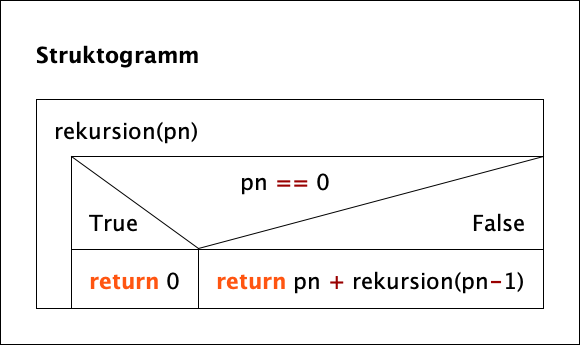
In der Abbildung 1 ist der iterative Algorithmus dargestellt und in der Abbildung 2 der rekursive Algorithmus.

In der Abbildung 3 ist in der Tabelle aufgeführt, wie im iterative Algorithmus die Summe von 1 bis 5 berechnet wird.
Wie die Berechnung der Summe von 1 bis 5 im rekursiven Algorithmus erfolgt, ist in der Abbildung 4 im Stackmodell dargestellt.


Funktion »iteration«
Der Funktion »iteration« liegt der in der Abbildung 1 dargestellte Algorithmus zugrunde. Die Funktion ist keine Callback-Funktion, sondern eine Funktion, die von der Callback-Funktion »einaus« das Programms »gauss2.py« aufgerufen und dadurch ausgeführt wird.
# iterative Funktion
def iteration(pn):
summe=1
for i in range(2, pn+1):
summe=summe+i
return summe
| 2. bis 6. Zeile | Die Funktion »iteration« mit dem formalen Parameter »pn« wird deklariert. |
| 3. Zeile | Der Variable »summe« wird zum Summieren der Startwert 1 zugewiesen. |
| 4. und 6. Zeile |
Die for-Schleife wird in die Funktion eingefügt.
|
| 6. Zeile | Der Rücksprung an die rufende Stelle erfolgt mit dem Wert der Variable »summe«. |
Funktion »rekursion«
Der Funktion »rekursion« liegt der in der Abbildung 2 dargestellte Algorithmus zugrunde. Die Funktion ist ebenfalls keine Callback-Funktion, sondern eine Funktion, die innerhalb der Callback-Funktion »einaus« des Programms »gauss2.py« aufgerufen und dadurch ausgeführt wird.
# rekursive Funktion
def rekursion(pn):
if pn==1:
return 1
else:
return pn+rekursion(pn-1)
| 2. bis 6. Zeile | Deklaration der Funktion »rekursion« mit dem formalen Parameter »pn«. |
| 3. bis 6. Zeile |
Die if-else-Anweisung mit zwei Bedíngungszweigen.
|
| 4. Zeile | Der Rücksprung an die rufende Stelle mit dem Wert 1. |
| 6. Zeile |
Rücksprung an die rufende Stelle mit dem Wert »pn+rekursion(pn-1)«.
|
Programm »gauss2.py«
Nachfolgend ist der Quelltext des Programms »gauss2.py« mit den Funktionen »iteration« und »rekursion«, der Callback-Funktion »einaus« und der grafischen Benutzeroberfläche – dem Hauptfenster mit Widgets – gegeben.
import tkinter as tk
# iterative Funktion
def iteration(pn):
summe=1
for i in range(2, pn+1):
summe=summe+i
return summe
# rekursive Funktion
def rekursion(pn):
if pn==1:
return 1
else:
return pn+rekursion(pn-1)
# Callback-Fumktion
def einaus():
try:
n=int(entry.get())
if n>0:
loesung1=iteration(n)
label2.config(\
text=f"Iterative Lösung ist {loesung1}")
loesung2=rekursion(n)
label3.config(\
text=f"Rekursive Lösung ist {loesung2}")
else:
label2.config(\
text="Die Ganzzahl n ist kleiner Eins!")
label3.config(text="")
except ValueError:
label2.config(text="Falsche Eingabe!")
entry.delete(0, tk.END)
# grafische Benutzeroberfläche
root=tk.Tk()
root.title("Summe der Ganzzahlen von 1 bis n(>0)")
root.geometry("400x280")
root.resizable(False, False)
# Widgets
label1=tk.Label(root, text="Gib eine Ganzzahl n>=0 ein!")
entry=tk.Entry(root, width=5)
button1=tk.Button(root, text="Summe", command=einaus)
label2=tk.Label(root, text="")
label3=tk.Label(root, text="")
button2=tk.Button(root, text="Programm beenden",\
command=root.destroy)
label1.pack(pady=10)
entry.pack(pady=10)
button1.pack(pady= 0)
label2.pack(pady=10)
label3.pack(pady=10)
button2.pack()
root.mainloop()
| 4. bis 8. Zeile | Deklaration derFunktion »iteration« mit dem formalen Parameter »pn«. |
| 11. bis 15. Zeile | Deklaration der Funktion »rekursion« mit dem formalen Parameter »pn«. |
| 18. bis 34. Zeile | Deklaration der Callback-Funktion »einaus«. |
| 19. bis 33. Zeile | Ausnahmebehandlung »,try« und »except« der Eingabe. |
| 20. Zeile |
Benutzereingabe einer Zeichenkette im Entry-Widget.
|
| 21. bis 31. Zeile | Eine »if-else-Anweisung« mit zwei Bedingungszweigen. |
| 22. Zeile |
Aufruf der Funktion »iteration« mit dem aktuellen Parameter »n«.
|
| 25. Zeile |
Aufruf der Funktion »rekursion« mit dem aktuellen Parameter »n«.
|
| 23., 24. und 26., 27. Zeile | Ausgaben der f-Srings (als Zeichenketten) auf Label-Widgets. |
| 34. Zeile | Löschen des Inhalts des Eingabefensters. |
Aufgabe A41
Implementiere das Programm »gauss2.py« am Computer.
Führe das Programm u. a. mit folgenden Eingaben aus und teste, ob es fehlerfrei läuft und den gestellten Anforderungen entspricht:
- 1
- 10
- 100
- 1000
Programm »fakultaet.py«
Iterative Definition:
- f1(n)=1, falls n=0
- f1(n)=1⋅2⋅ … ⋅(n-1)⋅n, falls n>0
Rekursive Definition:
- f2(n)=1, falls n=0
- f2(n)=f2(n-1)⋅n, falls n>0
Aufgabe A42
Implementiere ein Programm »fakultaet.py« am Computer.
Das Programm soll aus vier Teilen bestehen:
- der iterativen Funktion »f1«
- der rekursiven Funktion »f2«
- der Callback-Funktion »einaus«
- der grafische Benutzeroberfläche – dem Hauptfenster mit darauf platzierten Widgets
Führe das Programm u. a. mit folgenden Eingaben aus und teste, ob es fehlerfrei läuft und den gestellten Anforderungen entspricht:
- 0
- 1
- 5
- 10
In der folgenden Aufgabe wird auf das Programm »umdrehen.py« auf der Seite 3.4.1 eingegangen.
Aufgabe A43
Das umdrehen eines Wortes lässt sich einerseits – wie im Programm »umdrehen.py« – mit der rekursiven Funktion »reverse« lösen.
Andererseits könnte das umdrehen eines Wortes auch mit einer iterativen Funktion »reverse« gelöst werden:
Implementiere ein Programm »umdrehen2.py« mit einer iterativen Funktion »reverse« am Computer.
Führe das Programm u. a. mit folgenden Eingaben aus und teste, ob es fehlerfrei läuft und den gestellten Anforderungen entspricht:
- NEBEL
- LAGER
- LAGERREGAL
- LESE
- KAJAK
- RELIEFPFEILER
