Demoseite

3.4.1 Rekursives Programmieren

Mit der technischen Entwicklung des Kellerspeichers (Stackspeichers) in den 1950er Jahren wurde die Voraussetzung geschaffen, rekursiv zu programmieren. Während beim traditionelen iterativen Programmieren mit Schleifen – wie beispielsweise mit der for- oder while-Schleife – wiederholt wird, bedeutet Rekursion das Wiederholen mit Hilfe des Stackspeichers – sozusagen mittels eines »Gedächtnisses«. Dadurch wird es möglich, Probleme wie beim Turm von Hanoi, bei der Wegsuche im Labyrinth oder dem N-Damenproblem auf unkomplizierte Weise am Computer zu lösen.

Der Kellerspeicher

1957 entwickelten L. Bauer und K. Samelson den damals von ihnen als „Kellerspeicher“ (Keller) bezeichneten Stapelspeicher (Stack), wodurch das rekursive Programmieren möglich wurde.

Bild 69 — Abbildung 1, 2 und 3: Kellertreppe und Stack

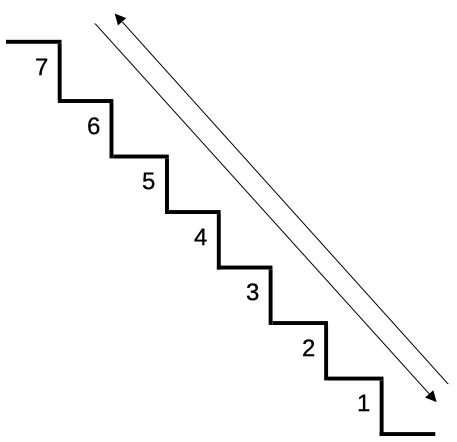
Bild 70 — Abbildung 1, 2 und 3: Kellertreppe und Stack

Es mag eigenartig anmuten, dass der in Abbildung 3 dargestellte Stack nach unten stapelt, wo doch beispielsweise Bücher nach oben aufeinander gestapelt werden.

Die Erklärung ist denkbar einfach.

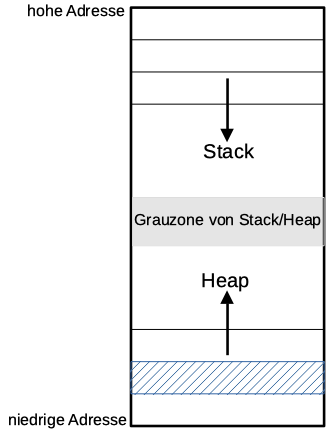
Der dynamische Speicherbereich Stack und Heap (Abbildung 4) ist technisch so organisiert, dass der Stack von oben (der hohen Adresse) nach unten (in Richtung der niedrigen Adresse) stapelt und der Heap von unten (der niedrigen Adresse) nach oben (in Richtung der hohen Adresse). Allerdings ist der Heap ein »besonderer Stapel«, der Lücken aufweisen kann, was beim Stack nicht der Fall ist.

Bild 72 — Abbildung 4: Dynamischer Speicherbereich

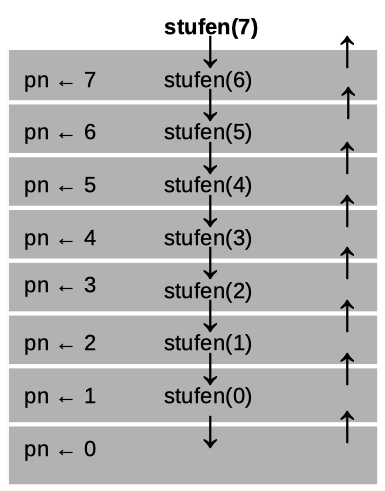
Programmiertechnisch wird die Rekursion in Python mit Funktionen umgesetzt.

Begriff »Rekursive Funktion«

Eine Funktion ist rekursiv, wenn sie sich mit veränderten Parametern selbst aufruft.

Quelltext des Programms »treppehoch.py«

# rekursive Funktion
def stufen(pn):
    if pn>0:
        print(f"Stufe {pn}")
        stufen(pn-1)

# Funktionsaufruf
stufen(7)

**Erklärung zum Quelltext**
2. bis 5. Zeile	Die rekursive Funktion »stufen« mit dem formalen Parameter »pn« wird deklariert. Der formale Parameter »pn« ist ein Platzhalter für den aktuellen Parameter, mit dem in der Funktion nach dem Aufruf gearbeitet wird.
3. bis 5. Zeile	Die if-else-Anweisung mit zwei Bedíngungszweigen. Ist der aktuelle Wert von »pn« größer als 0, dann ruft sich die rekursive Funktion selbst mit dem Wert »pn-1« als aktuellen Parameter auf. Die Selbstaufrufe der rekursiven Funktion enden, wenn der Wert von »pn« 0 ist.
4. Zeile	In der Python-Konsole wird im f-String (einer Zeichenkette) u. a.der Wert von »pn« ausgegeben.
4. und 5. Zeile	Beachte, dass innerhalb der Funktion der rekursive Selbstaufruf der Funktion nach der Ausgabe im f-String erfolgt.
8. Zeile	Die rekursive Funktion wird mit dem aktuellen Parameter 7 aufgerufen. Der aktuelle Parameter 7 wird an den formalen Parameter »pn« der Funktion übergeben.

Quelltext des Programms »trepperunter.py«

# rekursive Funktion
def stufen(pn):
    if pn>0:
        stufen(pn-1)
        print(f"Stufe {pn}")

# Funktionsaufruf
stufen(7)

**Erklärung zum Quelltext**
3. und 4. Zeile	Ist der aktuelle Wert von »pn« größer als 0, dann ruft sich die rekursive Funktion selbst mit dem Wert »pn-1« als aktueller Parameter auf. Die Selbstaufrufe der rekursiven Funktion enden, wenn der Wert von »pn« 0 ist.
4. und 5. Zeile	Beachte, dass innerhalb der Funktion der rekursive Selbstaufruf der Funktion vor der Ausgabe im f-String erfolgt.
5. Zeile	In der Python-Konsole wird im f-String (einer Zeichenkette) u. a. der Wert von »pn« ausgegeben.
8. Zeile	Die rekursive Funktion wird mit dem aktuellen Parameter 7 aufgerufen. Der aktuelle Parameter 7 wird an den formalen Parameter »pn« der Funktion übergeben.

Aufgabe A38

Gib die Ausgaben der Programme an:

»treppehoch.py«
»trepperunter.py«

Ein anschauliches Beispiel für Rekursion ist die Matroschka, die aus ineinander geschachtelten Puppen besteht. In der Abbildung 4 ist eine Matroschka dargestellt, die aus 5 unterschiedlich großen Puppen besteht. Die Puppen können der Größe nach ineinandergesteckt werden.

Quelltext des Programms »matroschka.py«

# rekursive Funktion
def puppen(pn):
    if pn > 0:
        print(f"Puppe {pn}")       
        puppen(pn-1)

# Funktionsaufruf
puppen(5)

Rekursives Programmieren ist eine »elegante« Art zu programmieren. Allerdings ist dieses Programmieren insofern schwierig, weil der Mensch im Allg, nicht rekursiv denkt.

Vorteile das rekursiven Progranmmierens:

ist u. a., dass die Quelltexte der Programme überschaubarer sind – insbesondere je umfänglicher die Quelltexte sind
es gibt Probleme, deren Lösungen sind nur sehr aufwendig iterarativ programmierbar – wie beispielsweise das N-Damenproblem oder die Wegsuche im Labyrinth
trotzdem gilt, dass jedes rekursiv lösbare Problem auch iterativ gelöst werdn kann und umgekehrt

Programm »umdrehen.py«

Das Programm leistet das Folgende:

(E)ingabe eines Wortes
(V)erarbeitung, indem die rekursive Funktion »reverse« die Reihenfolge der Buchstaben des Wortes durch Slicing (dt. schneiden) von Zeichenkette in Teilzeichenketten umkehrt (aus LAGER wird REGAI)
(A)usgabe des Wortes in der umgedrehten Reihenfolge der Buchstaben

Das Programm besteht aus drei Teilen:

der rekursiven Funktion »reverse«
der Callback-Funktion »ausein«
der grafischen Benutzeroberfläche – dem Hauptfenster mit darauf platzierten Widgets

Exkurs »Zeichenketten schneiden (slicing)«

Python ermöglicht durch Slicing (dt. schneiden) Teilzeichenketten aus Zeichenketten herauszulösen.

Ist beispielsweise der Wert der Variable »wort« die Zeichenkette "Informatik", dann bewirkt das Slicing:

wort[-1] das Herauslösen der Teilzeichenkette "k" aus der Zeichenkette "Informatik"
wort[:-1] das Herauslösen der Teilzeichenkette "Informarti" aus der Zeichenkette "Informatik"

Quelltext des Programms »umdrehen.py«

import tkinter as tk

# rekursive Funktion
def reverse(pwort):
    if pwort=="":
        return ""
    else:
        return pwort[-1]+reverse(pwort[:-1]) 

# Callback-Funktion
def einaus():
    wort=entry.get()
    wort=reverse(wort)
    label2.config(text=wort)
    entry.delete(0, tk.END)

# grafische Benutzeroberfläche   
root=tk.Tk()
root.title("Reverse")
root.geometry("400x250")
root.resizable(False, False)

# Widgets
label1=tk.Label(root, text="Gib ein Wort ein!")
entry=tk.Entry(root, width=20)
button1=tk.Button(root,\
                  text="Das Wort umkehren", command=einaus)
label2=tk.Label(root, text="")
button2=tk.Button(root, text="Programm beenden",\
                    command=root.destroy)

label1.pack(pady=10)
entry.pack(pady=10)
button1.pack(pady=10)
label2.pack(pady=10)
button2.pack()

root.mainloop()

**Erklärungen zum Quelltext**
4. bis 8. Zeile	Die rekursive Funktion »reverse« mit dem formalen Parameter »pwort« wird deklariert. Der formale Parameter »pwort« ist ein Platzhalter für den aktuellen Parameter mit dem in der Funktion gearbeitet wird.
8. Zeile	Die rekursive Funktion »reverse« ruft sich selbst mit dem veränderten aktuellen Parameter »pwort[:-1]« auf. Das heißt, mit dem Wort, aus dem der letzte Buchstabe herausgelöst ist. Mit Slicing »pwort[-1]« wird der letzte Buchstabe des in der Variable »pwort« abgelegten Wortes als Teilzeichenkette herausgelöst. Mit Slicing »pwort[:-1]« wird das in der Variable »pwort« abgelegte Wort ohne den letzten Buchstaben als Teilzeichenkette herausgelöst. Die Selbstaufrufe der rekursiven Funktion »reverse« enden, wenn der aktuelle Wert des formalen Parameters »pwort« das leere Wort "" ist (vergleiche Abbildung 6).
11. bis 15. Stelle	Die Callback-Funktion »einaus« wird deklariert.
13. Zeile	Die rekursive Funktion »reverse« wird mit dem aktuellen Parameter »wort« aufgerufen. Der aktuelle Parameter »wort« wird an den formalen Parameter »pwort« der rekursiven Funktion »reverse« übergeben.
14. Zeile	Das umgedrehte Wort wird ausgegeben. Da der Wert der Variable »wort« eine Zeichenkette ist, ist die Ausgabe in einem f-String nicht erforderlich.

In der Abbildung 6 ist das Stackmodell des Aufrufs »reverse("NEBEL")« der rekursiven Funktion »reverse« dargestellt.

Aufgabe A39

Implementiere das Programm »umdrehen.py« am Computer aus.

Führe das Programm u. a. mit folgenden Eingaben aus und teste, ob es fehlerfrei läuft und den gestellten Anforderungen entspricht:

LAGER
EIS
LESE
KAJAK
TOR

Palindrom

Begriff: Palindrom

Ein Palindrom ist eine Zeichenkette, die vorwärts und rückwärts gelesen identisch ist:

beispielsweise sind RENTNER, POP, TAT und GAG Palindrome

Aufgabe A40

Erweitere das Programm »umdrehen.py«, sodass geprüft wird, ob das durch die rekursive Funktion »reverse« umgedrehte Wort ein Palindrom ist.